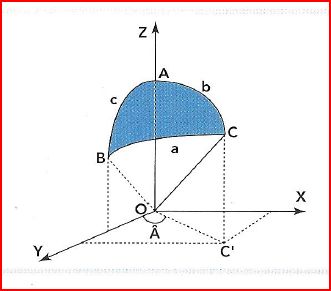
Définition du triangle sphèrique
Un triangle sphèrique est un triangle formé par 3 arcs de grand cercle.
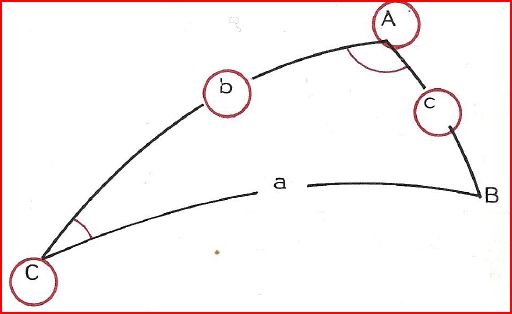
Le triangle ABC est un triangle sphèrique.
Les côtés d'un triangle sphérique sont des arcs de grand cercle. Leur longueur est exprimée en MN et sera égal à l'angle au centre de la Terre O exprimé en minutes d'arc. Ainsi toutes les longueurs peuvent être converties en angle (°, ', ") ou (°, ', '/100), et vice versa.
Attention: un trianle formé par 2 méridiens et un parallèle n'est pas un triangle sphérique. En effet, un parallèle (hormis l'équateur) n'est pas un grand cercle.
Coordonnées d'un point M sur une sphère de rayon 1
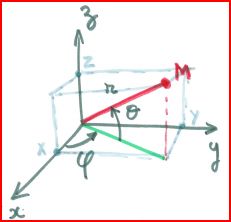
Dans le repère (O, x, y, z), les coordonnées de M sont:
\(\overrightarrow{OM}: \begin{vmatrix} \begin{align*}&X = cos\theta . cos\phi\\ &Y=cos\theta . sin\phi \\ &Z=sin\theta \end{align*} \end{vmatrix}\)
Formule fondamentale
Soit une sphère de rayon r=1
Si on joint les sommets du triangle sphérique au centre O de la sphère, alors, on obtient un trièdre dont les angles dièdres sont les angles du triangle.
Dans le repère (O, x, y, z), A est sur l'axe z, et B est sur le plan yOz, alors les coordonnées de B et de C sont:
\(\overrightarrow{OB}: \begin{vmatrix} \begin{align*}&X=0\\&Y=sinc\\&Z=cosc \end{align*} \end{vmatrix}\) et \(\overrightarrow{OC}: \begin{vmatrix} \begin{align*} &X'=sinb . sin\hat{A}\\&Y'=sinb . cos\hat{A}\\&Z'=cosb \end{align*} \end{vmatrix}\)
En calculant le produit scalaire de 2 façons différentes, nous avons:
\(\overrightarrow{OB} . \overrightarrow{OC} = \begin{align*} &\lbrace \Vert \overrightarrow{OB} \Vert. \Vert \overrightarrow{OC} \Vert \times cosa = 1 \times 1 \times cosa = cosa \\ &\lbrace XX'+YY' + ZZ' = sinc \space sinb \space cos\hat{A} + cosc \space cosb \\ \\ \Rightarrow &cosa = cosb . cosc + sinb . sinc . cosA\end{align*} \)
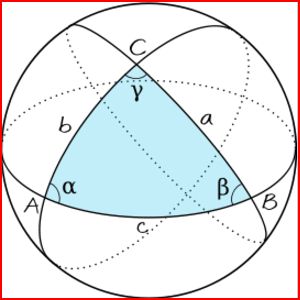
Soit ABC un triangle sphérique; a,b,c les distances associées; et \(\hat{A}=α\), \(\hat{B}=β\), \(\hat{C}=γ\), les angles au sommet. Alors:
\[\boxed {cosa = cosb \space cosc + sinb \space sinc \space cos\hat{A}}\]ou\[\boxed {cosa = cosb \space cosc + sinb \space sinc \space cosα}\]
Cette formule est valable pour tous les côtés du triangle sphérique.
Si vous voulez mémoriser cette formule fondamentale, je vous conseille de la considérer géométriquement. Il est plus facile de retenir "cos = coscos(côtés) + sinsin(côtés)cos(angle opposé)".
Analogie des sinus
Nous connaissons la formule fondamentale:
\(\begin{align*} cosa &= cosb . cosc + sinb . sinc . cos\hat{A} \\ \Rightarrow cos\hat{A}&=\frac{cosa-cosb . cosc}{sinb . sinc} \\ sin^2\hat{A} &=1-cos^2\hat{A} = 1-\frac{(cosa-cosb . cosc)^2}{sin^2b . sin^2c} \\&=\frac{sin^2b . sin^2c-(cosa-cosb . cosc)^2}{sin^2b . sin^2c} \\ &=\frac{(1-cos^2b)(1-cos^2c) -(cosa-cosb . cosc)^2}{sin^2b . sin^2c} \\ &=\frac{1-cos^2a-cos^2b-cos^2c+2cosa.cosb.cosc}{sin^2b . sin^2c} \\ \Rightarrow \frac{sin^2\hat{A}}{sin^2a}&=\frac{1-cos^2a-cos^2b-cos^2c+2cosa.cosb.cosc}{sin^2a.sin^2b.sin^2c} \\ \Rightarrow \frac{sin^2\hat{A}}{sin^2a}&=\frac{1-(cos^2a+cos^2b+cos^2c)+2cosa.cosb.cosc}{sin^2a.sin^2b.sin^2c} \end{align*}\)
Cette formule ne change pas par permutation des quantité a, b, et c en conséquence:
\(\frac{sin^2\hat{A}}{sin^2a}=\frac{sin^2\hat{B}}{sin^2b}=\frac{sin^2\hat{C}}{sin^2c}\)
a, b, c sont inférieurs à 180°, donc sina, sinb, sinc, sont positifs. On peut alors écrire:
\[\boxed{\frac{sinα}{sina}=\frac{sinβ}{sinb}=\frac{sinγ}{sinc}}\]ou\[\boxed{\frac{sin\hat{A}}{sina}=\frac{sin\hat{B}}{sinb}=\frac{sin\hat{C}}{sinc}}\]
Attention: cette formule ne fonctionne que si l'on sait si l'angle que l'on cherche est > ou < à 90°. En effet: \(sinγ = sin (180 - γ)\). Si il y a une ambiguité qui ne peut être levée de façon claire, alors il ne faut pas utiliser cette analogie des sinus.
Par exemple: si sinγ = 0,954 alors il y a 2 solutions
- γ = 72,55° et
- γ = 107,44°
Il faut, dans ce cas, préférer la formule des 4 éléments.
Formule des 4 éléments ou des cotangentes
Nous connaissons la formule fondamentale, aplliquons la aux côtés a et c:
\(cosa=cosb.cosc+sinb.sinc.cos\hat{A} \\ cosc = cosa.cosb+sina.sinb.cos\hat{C} \)
Remplaçons \(cosc\) dans la 1ère expression:
\(\begin{align*} cosa&=cosb.(cosa.cosb+sina.sinb.cos\hat{C}) +sinb.sinc.cos\hat{A} \\ &=cosa.cos^2b+cosb.sina.sinb.cos\hat{C}+sinb.sinc.cos\hat{A} \end{align*} \\ \Rightarrow cosa.(1-cos^2b)-cosb.sina.sinb.cos\hat{C} =sinb.sinc.cos\hat{A} \\ \Rightarrow cosa.sin^2b-cosb.sina.sinb.cos\hat{C} =sinb.sinc.cos\hat{A} \\ \Rightarrow \text{(1): } cosa.sinb-cosb.sina.cos\hat{C} =sinc.cos\hat{A} \space \text{ si } sinb \text{ différent de 0} \)
De même:
\(cosa=cosb.cosc+sinb.sinc.cos\hat{A} \\ cosb=cosa.cosc+sina.sinc.cos\hat{B} \\ \Rightarrow \text{(2): } cosa.sinc-cosc.sina.cos\hat{B} =sinb.cos\hat{A} \space \text{ si sinc différent de 0}\)
L'analogie des sinus nous donne:\(sina=\frac{sinc.sin\hat{A}}{sin\hat{C}}=\frac{sinb.sin\hat{A}}{sin\hat{B}}\)
Divisons (1) par la 1ère expression de \(sina=\frac{sinc.sin\hat{A}}{sin\hat{C}}\)
\(\Rightarrow cosa.sinb-cosb.sina.cos\hat{C} =sinc.cos\hat{A} \\ \Rightarrow \frac{cosa.sinb}{sina}-\frac{cosb.sina.cos\hat{C}}{sina} =\frac{sinc.cos\hat{A}}{sina} \\ \Rightarrow cotana.sinb - cosb.cos\hat{C}=\frac{sinc.cos\hat{A}.sin\hat{C}}{sinc.sin\hat{A}}\)
\(\Rightarrow \boxed{cotana.sinb = cotan\hat{A}.sin\hat{C}+cosb.cos\hat{C}}\)
Divisons (2) par la 2ème expression de \(sina=\frac{sinb.sin\hat{A}}{sin\hat{B}}\) , alors de même, nous trouvons:
\(\Rightarrow \boxed{cotana.sinc = cotan\hat{A}.sin\hat{B}+cosb.cos\hat{C}}\)
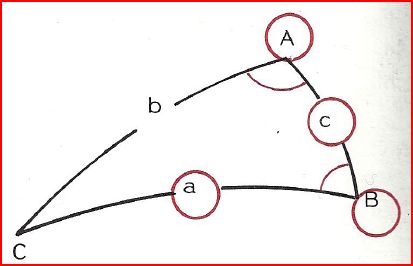
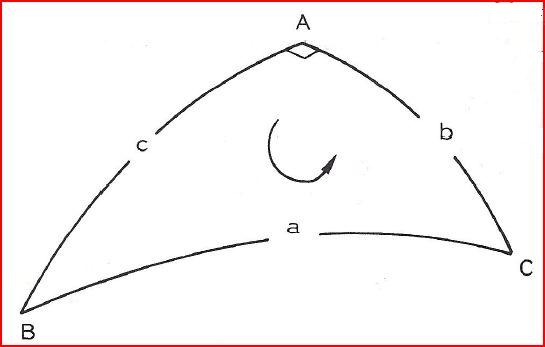
En utilisant toutes les formules fondamentales, il est possible d'écrire 6 formules des cotangentes, reliant 4 éléments consécutifs. Cette formule contient forcément 2 angles et 2 côtés.
Par exemple dans le triangle suivant, on a :
\(\boxed {cotan a \times sin c = cotan \hat{A} \times sin \hat{B} + cos c \times cos \hat{B}}\)
Il suffira de se rappeler la formule unique suivante:
\[\boxed {C_e \space S_i \space cotés = C_e \space S_i \space angles + Cos_i \space Cos_i}\]
avec:
- C = Cotangente = 1/tangente ( cotan(x) = tan(90-x))
- S = Sinus
- Cos = Cosinus
- e = extérieur
- i = intérieur
- les élements en bout de chaîne (a B c A) sont dits extérieurs (A et a)
- les 2 autres éléments sont dits intérieurs (B et c)
Application à un triangle rectangle (Le pentagone)
Un triangle sphérique est dit rectangle si un de ses angles α, β, γ est droit. On ne parle pas ici des longueurs a,b, c.
Si un côté (a,b,c) fait 90°, alors le triangle est dit rectilatère (recti = droit ; latère = côté).
Si un triangle est rectangle, alors les 6 formes de la formule des 4 éléments consécutifs se simplifient. En effet:
- cotan(90°) = 0
- sin(90°) = 1
- cos(90°) = 0
Dans ce cas, on peut utiliser la méthode du pentagone.
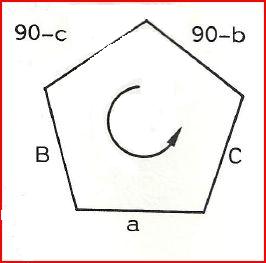
Le côté du bas représente l'hypoténuse du triangle rectangle.
Le cosinus d'un côté du pentagome est égal:
- au produit des sinus des côtès opposés
- au produit des cotan des côtés adjascents
\[\boxed { cos = sin(op) = cotan(adj)}\]
Pour rappel:
- sin(90-a) = cos a
- cos(90-a) = sin a
- cotan(90-a) = tan a
Ce qui nous donne alors:
- \(cos a = sin(90-c) . sin(90-b) = cosc . cos b\) et \(cos a = cotanB . cotanC\)
- \(cos B = sin(90-b) . sin(C) = cosb . sinC\) et \(cosB = cotan(90-c) . cotana = tanc . cotan a\)
- \(cos (90-c) = sinc = sina . sin(C)\) / \(cos(90-c) = sinc = cotan(90-b) . cotanB = tanb . cotan B\)
- etc, etc ,etc