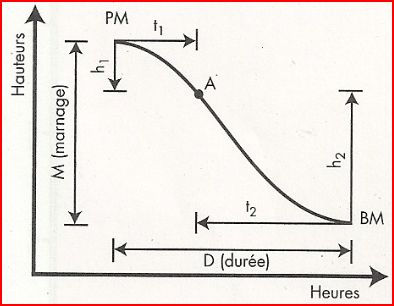
Le SHOM édite une formule mathématique. Elle est reprise dans le BMA2017. A condition d'avoir une bonne calculatrice, si possible programmable, il devient aisé de connaître la hauteur d'eau.
Il convient de remarquer la dépendance, à nouveau, à un système électrique, fonctionnant sur batterie. Cependant l'autonomie des batteries d'une calculatrice est suffisamment grande, et des piles de rechange peuvent être embarquées. Il existe aussi des calculatrices à énergie solaire.
On a :
pour calculer la hauteur d'eau au moment t1 ou t2: (1)
\(\mathrm {h_1 = M \times sin^2(\frac{90° t_1}{D})}\)
\(\mathrm {h_2 = M \times sin^2(\frac{90° t_2}{D})}\)
Pour calculer l'heure à laquelle on a une hauteur d'eau donnée: (2)
\(\mathrm {t_1 = \frac{D}{90} \times Arcsin \sqrt\frac{h_1}{M}}\)
\(\mathrm {t_2 = \frac{D}{90}\times sin^{-1} \sqrt\frac{h_2}{M}}\)
Pour utiliser ces formules, veillez à ce que votre calculatrice soit en mode "degré".
Application à nos 2 problèmes
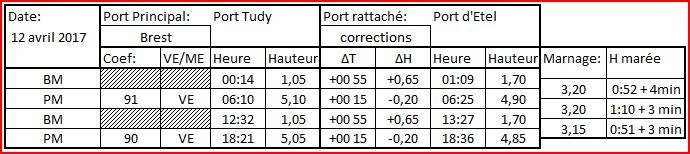
- Si j'ai besoin de 3 m d'eau pour quitter le port, à quelle heure pourrai-je partir ?
Je passe de BM à PM en 5h14, soit D=5.25 heures.
Il me faut 3 m d'eau pour quitter le port, soit h = 3.00 - 1.70 = 1.30 m au-dessus de BM et j'ai un marnage de M =3.20 m.
J'applique la formule (2) et je trouve: t = 2.30 heures soit 2h18 minutes après BM
La marée basse est à 01:09, j'aurai 3 m d'eau à 01h09 + 2h18 = 03h27, soit à 2 min prés le résultat du graphe des 12èmes
- Quelle sera la hauteur d'eau à 4h00?
A 04:00 je serai 2h25min avant PM soit 2.40 heures. J'applique la formule (1) avec M = 3.2 m, t = 2.40, D = 5.25.
Je trouve h = 1.38 m, soit une hauteur d'eau de 4.90 - 1.38 = 3.52 m, soit 3 cm d'écart avec le graphe des 12èmes.
Démonstration de la formule
La démonstration de la formule de calcul de la marée nécessite quelques préalables mathématiques.
Il faut avoir des connaissances relativement simples sur :
- la trigonométrie, les fonctions sinus et cosinus en particulier
- du calcul d'exponentiel
- la base des nombres complexes qui permettra de démontrer une formule de trigonométrie
- Les écritures exponentielle et trigonométrique d'un nombre imaginaire z = eix = cos(x) + isin(x)
- la partie réelle de z: R(z) = cos(x)
- la partie imaginaire de z: I(z) = sin(x)
- i² = i x i = -1
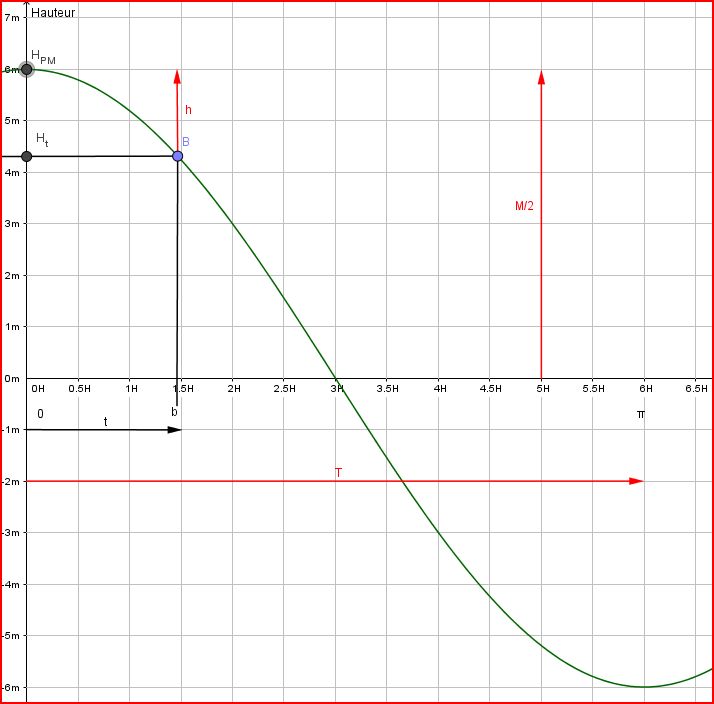
La hauteur d'eau varie autour de la hauteur d'eau moyenne dans le port de + M/2 à -M/2
La variation de hauteur d'eau à un moment t est h = HPM - Ht = M/2 cos(0) - M/2 cos(t) = M/2 x [cos(0) - cos(t) ]
Il nous faut donc calculer ΔH = [ cos(0) - cos(t) ]
Pour démontrer que \(\mathrm{cos(a) - cos(b) = -2sin(\frac{a+b}{2})sin(\frac{a-b}{2})}\) nous devons démontrer:
- \(\mathrm{cos(a+b) = cos(a)cos(b)-sin(a)sin(b)}\)
- \(\mathrm{cos(a-b) = cos(a)cos(b) + sin(a)sin(b)}\)
- par soustraction: \(\mathrm{cos(a+b) - cos(a-b) = - 2sin(a)sin(b)}\)
- En remplaçant a par \(\mathrm{\frac{a+b}{2}}\) et b par \(\mathrm{ \frac{a-b}{2}}\)
- trouver \(\mathrm{cos(a) - cos(b) = -2sin(\frac{a+b}{2})sin(\frac{a-b}{2})}\)
Vous pouvez voir la démonstration en bas de page ou encore vous reporter au "précis de trigonométrie" du chapitre navigation
Calculons la différence de hauteur ΔH = [cos(0) - cos(b) ]:
\(\mathrm{ΔH= cos(0) - cos(b) = -2sin(\frac{b}{2})sin(-\frac{b}{2})}\)
\(\mathrm{ΔH = 2sin^2(\frac{b}{2})}\)
et à l'instant t:
\( \mathrm {ΔH = 2 sin^2(\frac{t \times \frac{180°}{T}}{2})}\)
\( \mathrm {ΔH = 2 sin^2(\frac{90° \times t}{T}) }\)
Nous pouvons calculer h:
h = M/2 [cos(0) - cos(b) ] = M/2 x [ 2 sin²(90°t/T) ]
\[\mathrm {h = M \times sin^2(\frac{90° t}{T})}\]
avec :
- h = variation de hauteur d'eau après PM ou BM c'est à dire entre la PM et l'instant t.
- M = Marnage total sur la marée
- t = temps écoulé depuis PM ou BM
- T = Temps entre PM et BM donc le temps de la marée
Pour ceux qui ont suivi jusque la (les courageux!!!), le calcul du temps est simplement la fonction inverse de celle de la hauteur:
\(\mathrm {sin^2(\frac{90t}{T}) = \frac{h}{M}}\)
\(\mathrm {sin(\frac{90t}{T}) = \sqrt{\frac{h}{M}}}\)
\(\mathrm{\frac{90t}{T} = sin^{-1}(\sqrt{\frac{h}{M}})}\)
\[\mathrm {t = \frac{T}{90} \times Arcsin \sqrt\frac{h}{M}}\]
Formules d'addition: cos(a+b) = cos(a)cos(b)-sin(a)sin(b)
Connaissances nécessaires:
- Les nombres Complexes:
- eix=cos(x)+isin(x)
- la partie réelle de eix, R(eix) = cos(x).
Alors, on peut écrire:
cos (a+b) = R(ei(a+b)) (1)
= R(eia x eib)
Calculons eia x eib:
eia x eib = [ cos(a) + isin(a) ] x [ cos(b) + isin(b) ]
= cos(a)cos(b) + icos(a)sin(b) + isin(a)cos(b) - sin(a)sin(b)
= [ cos(a)cos(b) - sin(a)sin(b) ] + i[ sin(a)cos(b) + cos(a)sin(b) ]
Et extrayons la partie réelle R(eia x eib):
R(eia x eib) = cos(a)cos(b) - sin(a)sin(b) (2)
d'après (1) et (2) , alors:
cos (a+b) = cos(a)cos(b) - sin(a)sin(b) (3)
de même:
cos(a-b) = cos(a)cos(b) + sin(a)sin(b) (4)
Utilisons cette formule d'addition et calculons (3) - (4):
cos(a+b) - cos (a-b) = cos(a)cos(b) - cos(a)cos(b) - sin(a)sin(b) - sin(a)sin(b)
cos(a+b) - cos(a-b) = - 2sin(a)sin(b) (5)
Un petit remplacement de termes
En remplaçant a par \(\mathrm{ \frac{a+b}{2}}\) et b par \(\mathrm{ \frac{a-b}{2}}\) dans (5), il vient:
\(\mathrm{cos( \frac{a+b}{2} + \frac{a-b}{2}) - cos(\frac{a+b}{2}-\frac{a+b}{2}) = -2sin(\frac{a+b}{2})sin(\frac{a-b}{2})}\)
En remplaçant a par \(\mathrm{ \frac{a+b}{2}}\) et b par \(\mathrm{ \frac{a-b}{2}}\) (6)
La marée haute correspond à l'instant t = 0 (cos 0° = 1) donc a= 0
La marée basse correspond à l'instant t= 180 (cos180° = -1)
b correspond alors à l'instant \(\mathrm{t \times \frac{180°}{T}}\)