Loi fondamentale de la dynamique
Lorsqu'on veut étudier des mouvements de l'atmosphère dans son ensemble, il est commode de choisir un repère lié à la Terre et ayant son origine au centre de la Terre, et qui participe au mouvement diurne de rotation de la Terre sur elle même et à son mouvement annuel de rotation autour du Soleil.
Dans ces conditions, on peut appliquer la loi fondamentale de la dynamique:
\[\sum{ \overrightarrow{F} = m \overrightarrow{ \Gamma_a}}\]
Toutefois, à l'échelle synoptique à laquelle nous nous plaçons, il s'agit d'étudier le mouvement de l'air au voisinage d'une station, et il est plus commode d'utiliser un système d'axes dont l'origine est située à cette station.
Nous avons trouver l'accélération d'un mobile M dans un repère absolu:
\[\overrightarrow{\Gamma_a(M)} = \overrightarrow{\Gamma_r(M)} + \overrightarrow{\Gamma_c(M)} + \overrightarrow{\Gamma_e(M)}\]
avec:
- \(\overrightarrow{\Gamma_c(M)} = 2 \overrightarrow{\Omega} \wedge \overrightarrow{V_r(M)}\) représentant l'accélération de Coriolis
- \(\overrightarrow{\Gamma_e(M)} = \overrightarrow{\Gamma_a(o)} + \overrightarrow{\Omega} \wedge (\overrightarrow{\Omega} \wedge \overrightarrow{oM}) + \frac{d \overrightarrow{\Omega}}{dt} \wedge \overrightarrow{oM} \) représentant l'accélération d'entrainement
Ainsi,
\(\sum{\overrightarrow{F}}=m \overrightarrow{\Gamma_a}\)
\(\Rightarrow \sum{\overrightarrow{F}}=m(\overrightarrow{\Gamma_r(M)} + \overrightarrow{\Gamma_c(M)} + \overrightarrow{\Gamma_e(M)})\)
\(\Rightarrow \sum{\overrightarrow{F}}=m \overrightarrow{\Gamma_r(M)} +m \overrightarrow{\Gamma_c(M)} + m \overrightarrow{\Gamma_e(M)}\)
\[ \boxed{ \sum{\overrightarrow{F}} -m \overrightarrow{\Gamma_c(M)} - m \overrightarrow{\Gamma_e(M)}=m \overrightarrow{\Gamma_r(M)}}\]
- \( \sum{\overrightarrow{F}}\) représente la somme des forces directement appliquées au mobile M de masse m. Elles sont de 2 natures:
- \(\overrightarrow{F}\): force qui provoque le déplacement
- \(\overrightarrow{F_{aT}}\) : force d'attraction terrestre
- \( -m \overrightarrow{\Gamma_c(M)} = -2m \overrightarrow{\Omega} \wedge \overrightarrow{V}\) représente la force de CORIOLIS
- \( - m \overrightarrow{\Gamma_e(M)}\) représente les forces de d'entrainement.
Les forces d'entrainement
Nous avons démontré que: \[\overrightarrow{\Gamma_e(M)} = \overrightarrow{\Gamma_a(o)} + \frac{d \overrightarrow{\Omega}}{dt} \wedge \overrightarrow{oM} + \overrightarrow{\Omega} \wedge (\overrightarrow{\Omega} \wedge \overrightarrow{oM)}\]
Le rayon de courbure de l'orbite Terreste autour du Soleil est trés grand (\(\approx\) 150 000 000 kms) et le mouvement de la Terre sur cette orbite peut être considéré comme uniforme. Nous pourrons en conséquence négliger les accélérations dues à ce mouvement pratiquement rectiligne et uniforme. Il en résutlte que \(\overrightarrow{\Gamma_a(o)} = \overrightarrow{0}\)
Pour des périodes de temps relativement courtes, le mouvement de la Terre se résume à un mouvement de rotation sur elle même, autour de l'axe des pôles, qui est pratiquement constant. Il en résulte que \(\frac{d \overrightarrow{\Omega}}{dt} = \overrightarrow{0}\)
Et finalement \[\boxed{\overrightarrow{\Gamma_e(M)} = \overrightarrow{\Omega} \wedge (\overrightarrow{\Omega} \wedge \overrightarrow{oM)}}\]
Le mouvement de M est est mouvement circulaire uniforme. \(-m\overrightarrow{\Gamma_e}\) est donc la force centrifuge de module \(m \Omega^2 R\), expression classique de ce type de mouvement.
Composition de \(\overrightarrow{F_{aT}}\) et de \(-m \overrightarrow{\Gamma_e}\)
La force d 'entrainement est la force subie par M lorsqu'il est immobile dans oxyz, donc \(\overrightarrow{V_r(M)} = \overrightarrow{0}\).
Si M est immobile dans oxyz, alors M ne subit que son poids \(\overrightarrow{\Pi}\)
Il en résulte que \[\overrightarrow{\Pi} = \overrightarrow{F_{aT}}-m \overrightarrow{\Gamma_e} =m \overrightarrow{g}\]
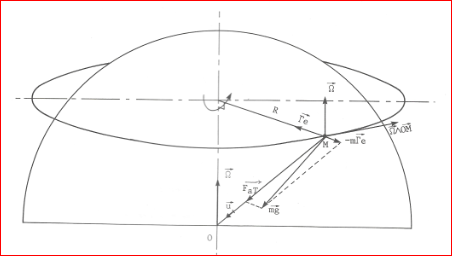
Conclusion
Nous pouvons écrire:
\[\boxed{\overrightarrow{F} + \overrightarrow{\Pi} - 2m\overrightarrow{\Omega} \wedge \overrightarrow{V_r(M)} = m \frac{d \overrightarrow{V_r(M)}}{dt}}\]
