La marée statique de Newton explique un certain nombre de phénomènes:
- La périodicité de la marée de 12 heures lunaires
- La relation entre l'amplitude de la marée et les phases de la Lune
- Le calcul des forces génératrices de la marée exercées par la Lune et le Soleil
Pourtant, cette théorie n'explique pas pourquoi:
- la Pleine Mer est en retard sur les syzygies (Pleine Lune ou Nlle Lune). En effet, la PM a lieu plus de 24 heures après la syzygie. Cette différence de temps s'appelle "l'âge de la marée" et peut être de 2 à 5 jours.
- l'importance des amplitudes le long des côtes avec un marnage de l'ordre de 15m en baie du Mont Saint-Michel.
Pierre-Simon Laplace (1749- 1823) est un mathématicien, astronome, physicien et homme politique français. Il introduit la notion de potentiel générateur de la marée.
- Le champ de la force génératrice de la marée dérive de ce potentiel générateur
- La définition de la marée: réponse du niveau marin à ce potentiel de marée qui prend la forme d’ondes diffuses
- qui se propagent à travers les océans avec une célérité dépendant de la profondeur,
- qui sont ensuite réfléchies, réfractées et dissipées,
- qui se superposent, interfèrent entre elles, renforçant ou atténuant certaines périodes.
C'est en 1775 que Laplace émet la théorie dynamique des marées avec 3 hypothèses principales:
- Principe des oscillations forcées : les masses d’eau soumises à une force périodique exécutent des oscillations de même période.
- Principe de la superposition des petits mouvements : le mouvement total d’un système soumis à de petites forces est égal à la somme des mouvements élémentaires.
- Le potentiel générateur est mathématiquement décomposable en 3 termes prépondérants:
- Groupe d’ondes de longues périodes (7j-18 ans),
- Groupe d’ondes de période diurne,
- Groupe d’ondes de période semi diurne,
La hauteur d'eau sera obtenue en faisant la somme de tous ces termes dépendant des conditions hydrauliques, donc de la forme arbitraire des continents et des irrégularités de la profondeur des océans, c'est-à-dire du lieu géographique.
\[h(t)=\sum_{i=1}^{n}A_{i} sin(ω_i t+φ_i)\] ce qui donne après les calculs:
\(h(t)= Bsin(Ωt+Φ)\) avec B=constante (linéarité)
Grâce à sa théorie dynamique, Laplace mettra au point une méthode de prédiction des marées. Antoine-Marie Chazallon (1801-1872), ingénieur hydrographe, sera à même
- d'éditer le "Pilote Français" et l'annuaire des marées avec comme port principal Brest et les ports secondaires rattachés par concordance (voir la méthode des concordances plus bas).
- de déterminer diverses ondes de la marée.
La formule de Laplace
- a servi pour l’annuaire des marées pendant plus de 150 ans et jusqu’en 1992!
- ne peut être utilisée que pour le port de Brest (c'est la raison pour laquelle vous trouverez les coefficients de marée uniquement pour le port de Brest...)
Aujourd’hui, on sait que cette formule ne peut être appliquée universellement car elle a comme hypothèse une linéarité de la formule (hors la marée diurne et les petits fonds n'ont pas de forme linéaire, elle ne peuvent donc pas correspondre a une formule linéaire telle que décrite par Laplace).
Les masses d'eau déplacées lors des marées conservent une certaine inertie, et la surface de la Terre présente de nombreux obstacles aux océans, comme des talus continentaux, ou des variations de profondeur. Les marées s'en trouvent alors accélérées ou au contraire freinées, et l'on observe ainsi, au fil des marées, des différences de marnage et de fréquence selon les régions. Les continents, par exemple, forment des barrières empêchant la marée de tourner autour de la Terre, et peuvent créer des effets de réfractions. C'est une des raisons pour laquelle l'onde de marée ne va pas, par exemple dans la Manche, d'Est en Ouest, mais d'Ouest en Est.
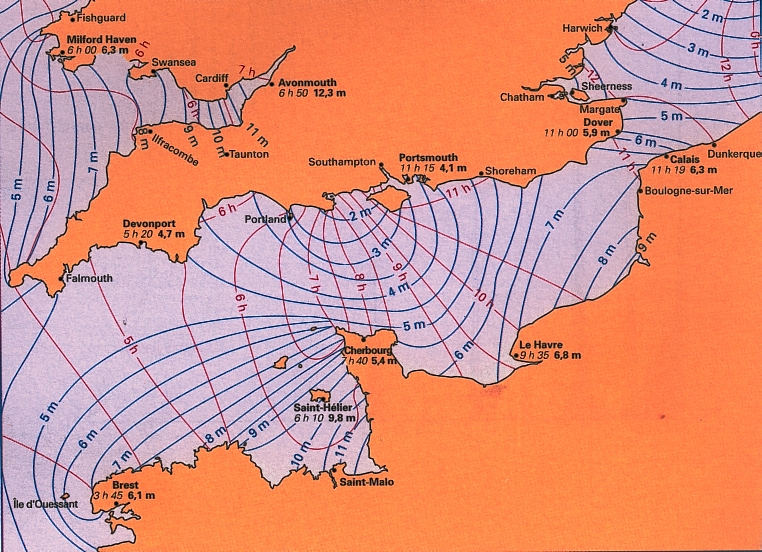
Cette carte représente l'évolution de la marée réelle dans la Manche (somme de toutes les composantes). Les nombres indiqués sous certains ports sont la phase de la pleine-mer et le marnage par vive-eau moyenne (coef=95). Les lignes représentent :
- en bleu : lignes d'iso-marnage représentant une égale valeur de marnage. C'est cette hauteur qui est utilisée pour le calcul du coefficient de marée. Notez que la marée est plus importante le long des côtes françaises que des côtes anglaises, cela est du à la force de Coriolis qui tend à pousser l'onde vers la droite.
- en rouge : les lignes cotidales représentant les points se trouvant en pleine-mer (PM) à la même heure. Si la PM est à 3h45 à Brest, la marée est encore montante à Cherbourg, et la PM à Cherbourg ne sera atteinte qu'à 7h40, soit presque 4h après. L'onde de marée se propage vers le Pas de Calais.
On sait aujourd'hui que La théorie de Laplace, si elle peut fonctionner sur nos côtes, n'est pas suffisante pour calculer avec suffisamment de précision la marée. Pourtant d'autres scientifiques travailleront avec cette formule.
Une autre méthode sera mise au point: c'est la méthode de la formule Harmonique et des ondes de marée.

