Si le passage des coordonnées Horaires aux coordonnées Equatoriales, et vice versa, est simple, c'est un peu plus compliqué pour passer des coordonnées Horizontales aux coordonnées Horaires.
Pour se faire, il suffit de résoudre un triangle sphérique grâce à la trigonométrie sphérique (voir le chapitre Calcul orthodromique et au Précis de trigonométrie).
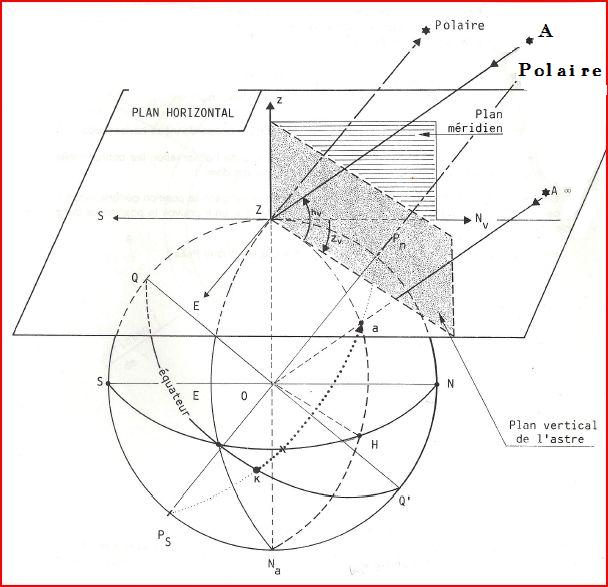
Voici la situation générale:
Il faudra résoudre le triangle Pn-A-Z en connaissant les données suivantes:
- l'heure (qui nous donnera la position du pied de l'astre (le GHA et la déclinaison, lus dans les éphémérides)
- Zv = azimut vrai mesuré par l'observateur
- Hv = hauteur vraie mesurée par l'observateur
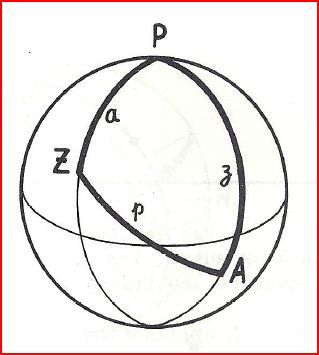
Identifions le triangle P, Z, A p, z, a:
- p: distance zénithale N avec N+Hv = 90 donc N = 90-Hv
- z = 90 - D (déclinaison de l'astre avec D>0 si Nord et D<0 si Sud)
- a = 90-L (L= latitude de l'observateur)
- P = LHA ou 360 - LHA en fonction des configurations
- Z = Zv
- A
Calcul de H et de Z
C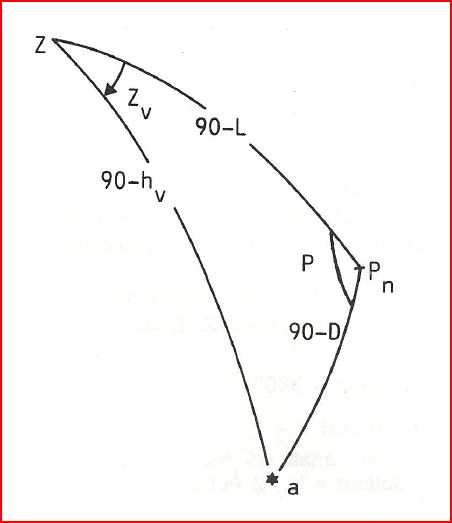
e qui nous donne le triangle ci-contre, dans lequel en fonction des éléments connus, on peut appliquer les formules de trigonométrie sphérique.
- pour déterminer une hauteur H:
Appliqueons la formule fondamentale:
\(cos (90-H) = cos(90-L) cos(90-D) + sin(90-L) sin(90-D) cosP\)
\(\Rightarrow \boxed{sinH = sinL sinD + cosL cosD cosP}\)
- pour déterminer l'azimuth Z:
Appliquons la formule des 4 éléments consécutifs:
\(C_e \space S_i \space cotés = C_e \space S_i \space angles + Cos_i \space Cos_i\)
\(\Rightarrow cotan(90-D)sin(90-L)= cotanZ sinP + cos(90-L) cosP\)
\(\Rightarrow cotanZ sinP= cotan(90-D)sin(90-L)-cos(90-L)cosP\)
\(\Rightarrow tan(90-Z) sinP = tanDcosL-sinLcosP\)
\(\Rightarrow \boxed{tan(90-Z) = \frac{tanDcosL-sinLcosP}{sinP}}\)
Vous remarquerez qu'il est nécessaire de connaître l'angle P pour trouver H et Z.