Nous avons démontré que \(\overrightarrow{\Gamma_c} = 2 \overrightarrow{\Omega} \wedge \overrightarrow{V}\)
En conséquence, la Force de Coriolis \(\overrightarrow{F_c} = -m \overrightarrow{\Gamma_c} = -2m \overrightarrow{\Omega} \wedge \overrightarrow{V}\)
La force de Coriolis est donc perpendiculaire au plan formé par les vecteurs \(\overrightarrow{\Omega}\) et \(\overrightarrow{V}\)
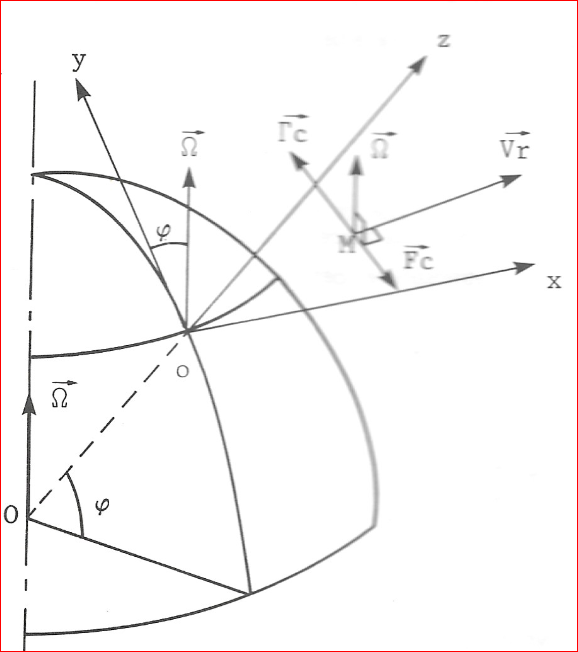On pourra noter dans le repère oxyz :
\(\overrightarrow{V_r} \pmatrix{u \\ v \\ w }\)
\(\overrightarrow{\Omega} \pmatrix{0 \\ \Omega.cos\varphi \\ \Omega.sin\varphi }\)
\(\overrightarrow{F_c} = -2m \overrightarrow{\Omega} \wedge \overrightarrow{V} =-2m \pmatrix{0 \\ \Omega.cos\varphi \\ \Omega.sin\varphi } \wedge \pmatrix{u \\ v \\ w }\)
\(\overrightarrow{F_c} = -2m \pmatrix{0 \\ \Omega.cos\varphi \\ \Omega.sin\varphi } \wedge \pmatrix{u \\ v \\ w }\)
\(\overrightarrow{F_c} = \pmatrix{-2m \Omega (w.cos \varphi - v.sin \varphi)0 \\-2m \Omega.u.sin\varphi \\+2m \Omega.u.cos\varphi }\)
On remarque que la composante de \(\overrightarrow{F_c}\) selon l'axe oy dépend de la latitude:
- Latitude Nord (\(\varphi>0 \Rightarrow sin\varphi >0 \Rightarrow Fc_y <0\)), la composante de la force de Coriolis est négative, et est à droite de la vitesse. M est dévié vers la droite
- Latitude Sud (\(\varphi<0 \Rightarrow \sin\varphi < 0 \Rightarrow Fc_y > 0\)), la composante de la force de Coriolis est positive, et est à gauche de la vitesse. M est dévié vers la gauche