Les fonctions de Dieumegard

Les tables de Dieumegard permettent de trouver Hc.

On pourra connaître l'intercept en calculant la différence entre Hv et Hc

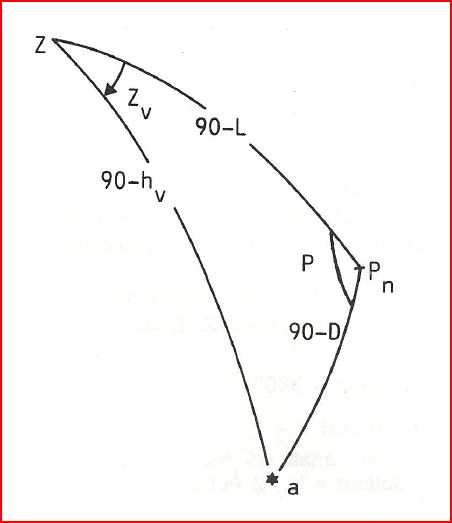
Soit la formule fondamentale: 

cos(90-Hc) = cos(90-L) cos(90-D) + sin(90-L)  sin(90-D) cosP

Dieumegard a écrit cette formule sous une autre forme. Cette nouvelle forme va permettre de rentrer dans des tables précalculées afin de nous rendre le calcul plus facile.

Pour la suite, je vous conseille de vous référer au précis de trigonométrie.

La formule de Dieumegard

Nous savons que :

(1) cos(90-H_C) = cos(90-L) cos(90-D) + sin(90-L) sin(90-D) cosP

(2) cosa cosb = cos(a-b) - sina sinb car cos(a-b) = cosa cosb + sina sinb

(3) sin(90-a) = cosa

(4) cos(-a) = cosa

(5) cosa cosb = cos(a+b) + sina sinb car cos(a+b) = cosa cosb - sina sinb

Partons de (1) et modifions cette formule avec nos connaissances trigonométriques:

(1) cos(90-H_C) = cos(90-L) cos(90-D) + sin(90-L) sin(90-D) cosP

(2) \(\Rightarrow\) cos(90-H_C) = cos(90-L-90+D) - sin(90-L) sin(90-D) + sin(90-L) sin(90-D) cosP

(3) \(\Rightarrow\) cos(90-H_C)= cos(- L + D) - cosL cosD +cosL cosD cosP

factorisation \(\Rightarrow\) cos(90-H_C) = cos(-(L-D)) + cosL cosD (-1+cosP)

(4) \(\Rightarrow\) cos(90-H_C) = cos(L-D) + cosL cosD (-1+cosP)

multiplier par (-1) de chaque côté: \(\Rightarrow\) -cos(90-H_C) = -cos(L-D) + cosL cosD (1-cosP)

ajouter 1 de chaque côté: \(\Rightarrow\)  [1-cos(90-H_C)] =[1- cos(L-D)] + [cosL cosD (1-cosP)]

 \[\boxed {\text{Formule de Dieumegard:} \\ \lbrack1-cos(90-H_c) \rbrack=\lbrack1- cos(L-D)\rbrack + \lbrack cosL \times cosD \times (1-cosP)\rbrack}\]

Remarque:

Une autre façon d'exprimer ce résultat est:

1 - sinHC = 1 - cos(L-D) + cosL cosD (1-cosP)

A la place de (2) , nous aurions pu utiliser (5), et en utilisant les mêmes proriétés et procédés,  nous aurions alors obtenu:

1 + sinHc = 1 - cos(L+D) + cosL cosP (1 + cosP)

ce qui en créant une table qui irait bien permettrait de vérifier les calculs.

Remarques sur la formule de Dieumegard

La formule de Dieumegard peut se résumer à: (1- cosα) = (1- cosβ) + cosγ cosδ (1- cosε)

On remarque dans la formule de Dieumegard de deux fonctions ou formes élémentaires:

• 1- cosα
• cosα

On remarque aussi que:

• cosL < 1,
• cosD < 1,
• 0 < 1-cosP < 2

 Multiplier ces 3 termes  sans calculatrice

• serait compliqué (sans calculatrice, l'addition est préférable à la multiplication)
• donnerait un chiffre trés petit,
• et donc, les calculs perdraient en précision. 

Pour éviter cela, on passe par du calcul logarithmique pour calculer la forme cosγ cosδ (1- cosε). Voici quelques règles du calcul logarithmique:

1. log ne peut pas avoir comme argument un nombre négatif ou nul. (log(-2) n'existe pas!!, ni Log(0)!!)
2. 10^log(a)=a, c'est la fonction inverse de la fonction log
3. log(a x b) = loga + logb. Il est possible de transformer une multiplication par une addition ce qui rendra les calculs à la main plus faciles
4. log(1/a) = log(a^-1) = -log(a)

Vérifions la Régle 1:

-90<L<90 \(\Rightarrow\) cosL>0

-90<D<90 \(\Rightarrow\) cosD>0

cosP<1 \(\Rightarrow\) (1-cosP)>0

\(\Rightarrow\) cosL cosD (1-cosP) >0, on peut donc utiliser cette expression dans un logarithme.

Appliquons la Régle 2

Soit le produit p = cosL x cosD x (1-cosP)

p = 10^{log(CosL x CosD x (1-cosP))}

p = 10^{- ( -log(CosL x CosD x (1-cosP)))}

Appliquons la Régle 3

p = 10^{- ( -log(CosL) -log(CosD) - log( 1-cosP))}

p = 10^{- ( -log(CosL) + (-log(CosD)) +  (- log( 1-cosP)))}

Nous avons transformé notre multiplication en:

• 3 additions
• 1 fonction 10^-x

Les fonctions de Dieumeguard

Afin de calculer Hc nous aurons besoin de 4 fonctions:

• f(x) = -log(1-cosx) \(\Rightarrow\) f(P) = -log(1-cosP)
• g(x) = -log(cosx) \(\Rightarrow\) g(L) = -log(cosL) et g(D) = -log(cosD)
• h(x) = 10^-x
• i(x) = 1-cosx \(\Rightarrow\) i(90 - Hc) = 1 - (cos90-Hc) et i(L-D) = 1-cos(L-D)

alors :

• cosL x cosD x (1-cosP) = h [g(L) + g(D) + f(P)]
• 1-cos(90-H_C) = i(90-H_C)
• 1-cos(L-D) = i(L-D)

Et la formule de Dieumegard s'écrit:

\[\boxed{i(90-H_c) = i(L-D) + h\lbrack g(L)+g(D)+f(P)\rbrack}\]

Nous avons donc besoin de 4 tables représentant ces 4 fonctions pour résoudre cette équation 

• Table 1 : f(x) = -log(1-cosx) pour trouver a1
• Table 2 : g(x) = -log(cosx) pour trouver a2 et a3
• Table 3 : h(x) = 10^-x pour trouver a4 (a2 + a3 +a1) = a4(S1)
• Table A : i(x) = 1-cosx pour trouver a5 et Hc enfonction de S2 = a5 + a4

Elements des Tables de Dieumegard

Les paramêtres entrant dans les tables varient:

• -90 < D < +90
• -90 < L < +90
• -180 < P < +180
• 0 < LHA < 360
• 0 < H < 90
• 0 < Z < 360

Afin de réduire le nombre important de pages nécessaires pour représenter les fonctions de Dieumegard et Bataille, nous allons devoir les étudier un peu plus en détail, trouver des symétries (division par 2 du nombre de page), utiliser des propriétés trigonmétriques comme sin(90 - x) = cosx ou cos(90 - x) = sinx, ou encore cotan(90 - x) = tanx..........

Les tables de Dieumegard permettent de calculer Hc. Un angle de 1' représentant un écart de 1 mille nautique, les calculs devront être assez précis. En conséquence, ces tables seront éditées avec 4 chiffres après la virgule.