La projection Lambert

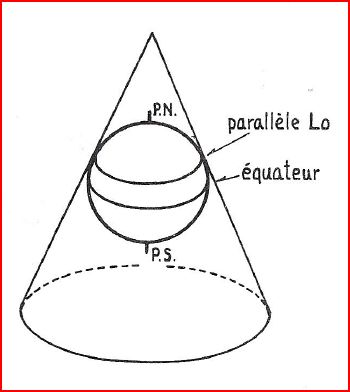
On cherche à construire une carte rigoureusement conforme et pratiquement orthodromique au voisinage d'un parallèle L₀, que l'on se fixe.

Une carte orthodromique est une carte sur laquelle une orthodromie est représentée par une droite.

Etude du canevas

Le canevas Lambert est construit à partir

• d'une projection géométrique,
• depuis le centre de la sphère réduite,
• sur un cône tangent à cette sphère
• le long d'un parallèle L₀

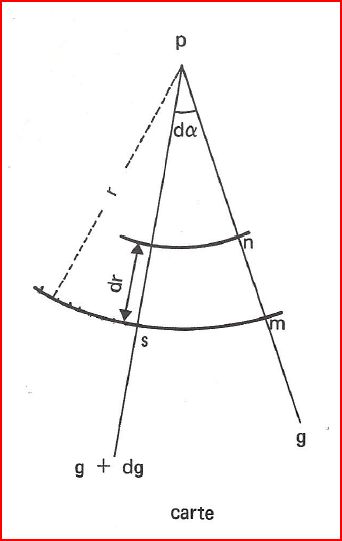
Commençons par placer:

• le Pôle
• un méridien
• un arc de cercle centré sur le pôle qui représentera le parallèle L₀

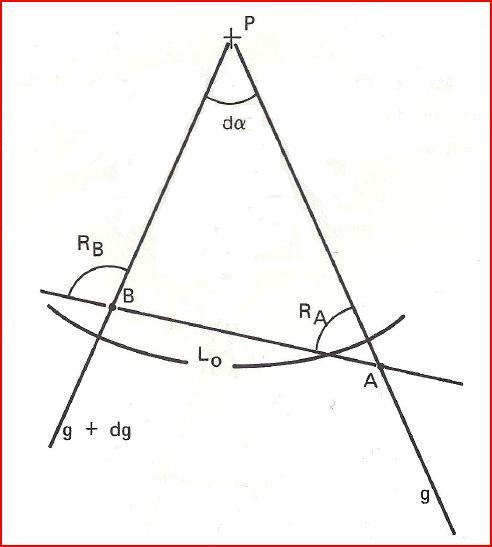
Essayons de placer le méridien de longitude g+dg. Pour cela considérons 2 points:

• A (g; Lo-dL)
• B (g+dg; L₀+dL)

La droite AB étant trés proche de L₀ devra représenter l'orthodromie.

Sur la Terre, la variation d'angle de route orthodromique entre A et B est égale à la convergence des méridiens:

R_B-R_A= dg x sin Lm avec Lm=L₀

Sur la carte, R_B-R_A = dα

donc:  \[ \boxed { dα = dg \times sinL_0}\]

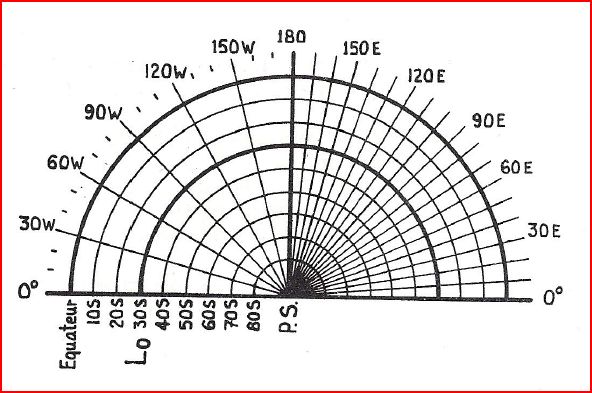
Comme sinL₀ < 1, une carte Lambert couvrant un écart de 360° de longitude sera représentée par un secteur angulaire inférieur à 360°. Et cette carte ne sera pas conforme au pôle. 

Par exemple voici

• un canevas Lambert tangent en 50°N (L₀ =50N) : dα = 360 x sin 50  = 276°
• un canevas Lambert tangent en 30°S (L₀ =30S) : dα = 360 x sin 30  = 180°

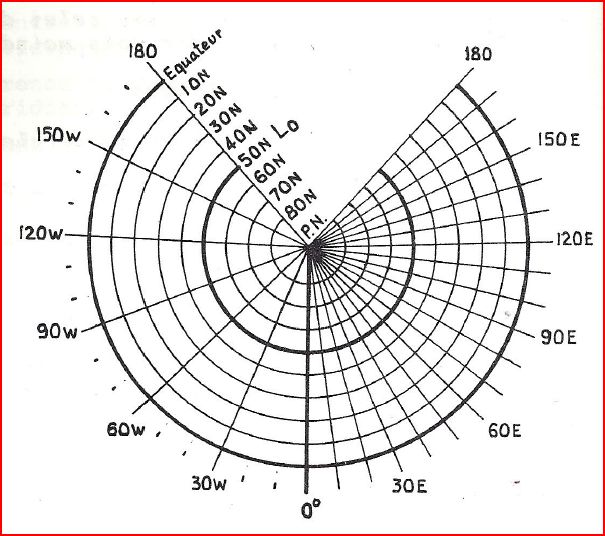
Essayons maintenant de placer les parallèles

Nous voulons que le canevas soit rigoureusement conforme, Pour cela, il faut que \(E_p = E_m\).

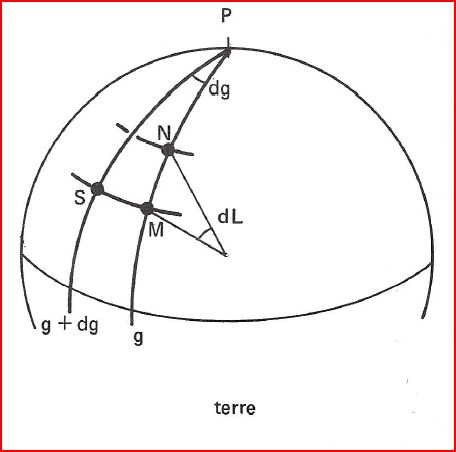
soient 3 points sur la Terre:

• M (g;L)
• N (g;L+dL)
• S (g+dg;L)

représentés sur la carte par m, n, s

(1) \(E_m = \frac{mn}{MN} = -\frac{dr}{R\times dL}\) (signe moins car si L augmente, r diminue)

(2) \(E_p = \frac{ms}{MS} =\frac{r \times dα}{R \times dg \times cosL}\)

(1) = (2) \(\Rightarrow \frac{dr}{R\times dL} = - \frac{r \times dα}{R \times dg \times cosL}\)

posons \(C= \frac{\pi}{2}-L \Rightarrow dL=-dC\) et \(cosL = sinC\)

C est la colatitude du parallèle de latitude L

nous avons alors \(\frac{dr}{r} = \frac{dα \times dC}{dg \times sinC}\)

hors dα = dg sinL₀

\(\frac{dr}{r} = sinL_0 \times \frac{dC}{sinC}\) et si n= sinL₀

\(\frac{dr}{r} = n \times \frac{dC}{sinC}\)

En intégrant cette équation, il vient:

\(Log\frac{r}{K} = n Log(tan\frac{C}{2}) = Log(tan\frac{C}{2})^n\)

\(r=K(tan\frac{C}{2})^n\)

Il nous reste à déterminer la constante K. Pour cela disons que C/2 = 45°

alors \(tan45 = 1\) et \(1^n=1\), et dans ce cas \(r=K\)

si C/2 = 45 alors C = 90° = π/2

et comme on a fixé C = π/2 - L, alors L = 0 et donc r = r_E = rayon image de l'équateur.

Donc: \[\boxed{ r = r_E ( tan\frac{C}{2})}\] avec C = colatitude du parallèle de laitude L.

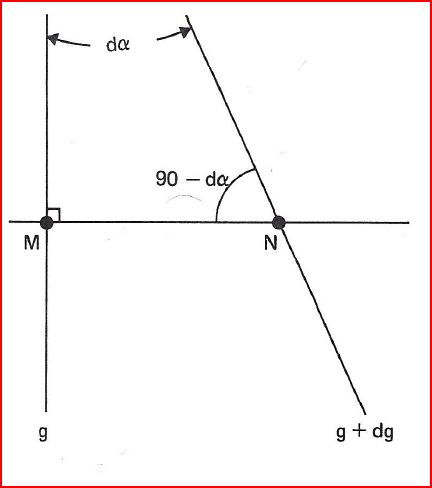
Détermination rapide de L₀

On sait que \(sinL_0 = \frac{dα}{dg}\)

• Choisir 2 méridiens suffisemments espacés ce qui permettra une mesure plus précise
• En un point M quelconque appartenant à un méridien, tracé une perpendiculaire
• Cette perpendiculaire coupe l'autre méridien en N

L'angle en N vaut 90 - dα, d'où on tire α

Mesure de distance entre 2 points

Proceder comme sur la carte Mercator. 

Reporter la distance autour de la latitude moyenne entre A et B, le long d'un méridien.

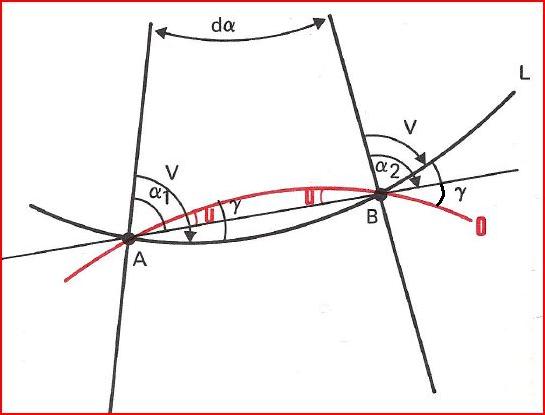
Angle u entre ortho et droite carte ou pseudo correction de Givry

(1) en A: α₁ = V - γ + u

(2) en B: α₂ = V + γ - u

α₁ - α₂ = -2γ + 2u

or α₂ = α₁ + dα = α₁ + dg x sinL0

Donc:

α₁ - α₂ = α₁ - α₁ - dg x sinL₀ = 2u - 2γ = 2u - dg x sinL_m

2u = dg x sinL -  dg x sinL₀

\[\boxed{u = \frac{dg}{2}(sinL_m - sinL_0)}\]

Angle δ entre loxo et droite carte

L'angle entre otho et loxo = correction de Givry  = γ

(1) \(γ = \frac{dg}{2}sinL_m\)

(2) \(u = \frac{dg}{2}(sinL_m - sinL_0)\)

or \(δ = γ -u = \frac{dg}{2} \times sinL_0\)

\[\boxed{δ = \frac{dg}{2} \times sinL_0}\]

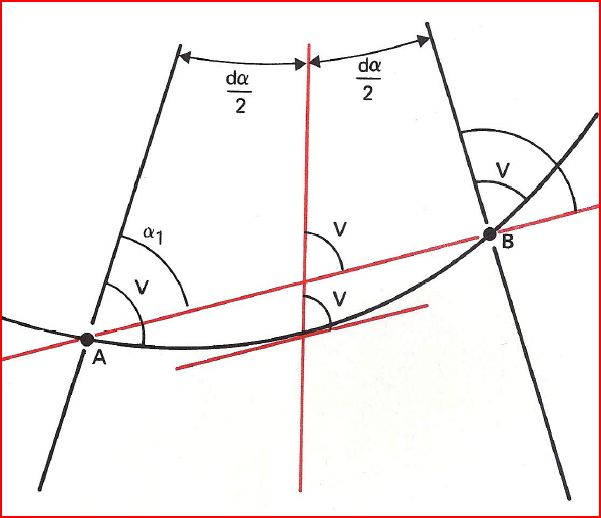
Mesure d'une route entre 2 points

Pour déterminer la route à adopter pour aller de A à B, on a besoin de connaître la route vraie moyenne entre ces 2 points. Or quelque

soit la trajectoire suivie, la route moyenne entre 2 points est toujours égale à la route loxodromique. D'où l'intérêt de savoir mesurer rapidement la route loxodromique entre 2 points.

• Traçons le méridien central entre A et B
• Traçons la droite AB
• la tangente à la loxodromie sur le méridien central est parallèle à la droite AB
• En mesurant sur le méridien central l'orientation de la droite AB, on trouve la R_V loxodromique

On peut aussi se contenter de mesurer les angles α_{1 et} α₂ et dire: 

\(α_1 = V - \frac{dα}{2}\)

\(α_2 = V + \frac{dα}{2}\)

et donc :

\[\boxed { V = \frac{α_1 + α_2}{2} }\]

Ensuite , on connait γ, β, δ, u........