Pour mémoire, la formule originale est:
\[\boxed{1 - cos(90 - Hc) = 1 - cos(L - D) + cosLcosD(1-cosP)}\]
La formule de Dieumegard s'écrit:
\[\boxed{i(90-H_c) = i(L-D) + h\lbrack g(L)+g(D)+f(P)\rbrack}\]
ou encore en écriture simplifiée:
\[\boxed{Hc = a5 + a4(a2 +a3 +a1)}\]
Nous avons donc besoin de 4 tables représentant 4 fonctions pour résoudre cette équation
- Table 1 : f(x) = -log(1-cosx) pour trouver a1
- Table 2 : g(x) = -log(cosx) pour trouver a2 et a3
- Table 3 : h(x) = 10-x pour trouver a4
- Table A : i(x) = 1-cosx pour trouver a5 et Hc
Table 1 pour trouver la valeur a1 = -log(1 - cosP)
Remarques préliminaires:
Log(x) avec x < 0 et x = 0 n'existe pas, et log(x) tend vers l'infini si x tend vers 0.
- Si P = 0 alors cosP = 1, 1 - cosP = 0, et donc Log(1-cosP) n'existe pas. Il sera donc impossible de faire le point au midi local. De façon générale, le point autour du midi local manquera de précision. A ce moment, il sera préférable de faire le point par la méridienne.
- Si 0 < LHA < 090, cosP > 0 , 1 - cosP < 1 et -Log(1 - cosP) > 0
- Si 270 < LHA < 360, cosP > 0 , 1 - cosP < 1 et -Log(1 - cosP) > 0
- Si 090 < LHA < 270, cosP < 0 , 1 - cosP >1 et -Log(1 - cosP) < 0
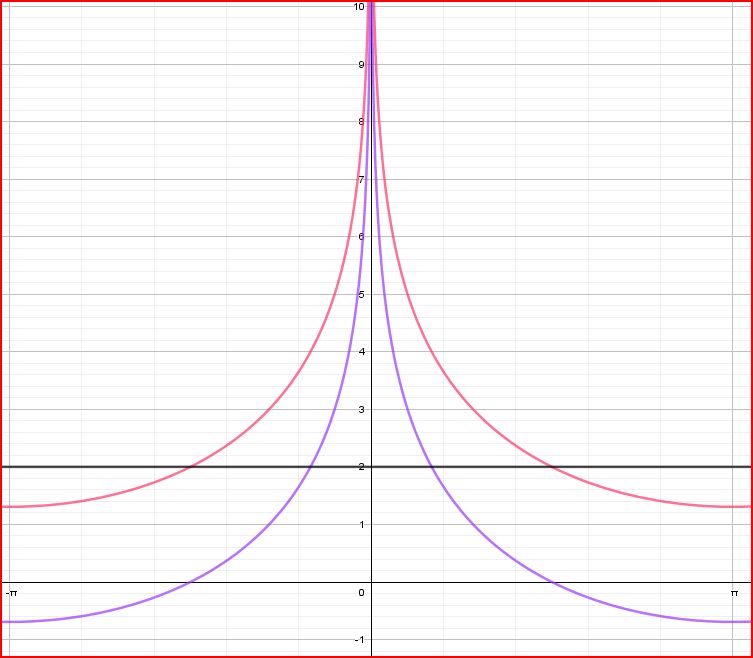
Regardons le tracé de la fonction y = -Log(1-cosP), la courbe bleue
(Tracé des fonction -Log(1-cosP) en bleu et de 2 - Log(1-cosP) en rouge)
Symétrie par rapport à P = 0
cos(-x) = cos(x) (on dit que la fonction est paire). Alors:
-Log (1 - cosP) prendra les mêmes valeurs, que P soit positif ou négatif, pour 0 < LHA < 180 et pour 180 < LHA < 360.
Le tableau des valeurs sera donc symétrique par rapport à P = 0.
En conséquence:
- Horizontalement, les degrés de LHA
- l'entrée dans la partie haute des tableau ira de 180 à 359° (le matin avec LHA > 180 et astre à l'Est)
- l'entrée dans la partie basse du tableau ira de 0 (la case est vide car la valeur log(0) n'existe pas ) à 179° (le soir avec LHA < 180 et astre à l'Ouest)
- Verticalement, les minutes de LHA
- colonne de gauche pour LHA > 180
- colonne de droite pour LHA > 180 (au matin de l'astre)
- On lira le résultat dans la "case intercection" des degrés et minutes, à l'interieur du tableau, -Log(1 - cosLHA)
La somme de 3 termes
nous souhaitons, pour faciliter les calculs, additionner facilement 3 termes a1, a2, a3. or:
- Si 090 < LHA < 270, cosP < 0 , 1 - cosP >1 et -Log(1 - cosP) < 0
On introduit ici un nombre négatif dans la somme a2 + a3 + a1 avec a1 < 0, ce qui est peu aisé à calculer. Il faut trouver une solution pour transformer cette opération en une opération plus simple à faire.
Pour remédier à cela, nous allons ajouter -1 et le complément à 1 de -Log(1-cosP), ce qui nous amènera à avoir la somme de 3 nombres positifs a laquelle il faudra retirer 1. Ce qui est bien plus aisé que de faire une soustraction d'un nombre à 4 décimales.
Prenons par exemple -Log(1-cos180) = -0.3010 (courbe bleue). a2 + a3 - 0.3010 est compliqué à calculer.
Alors le complément à 1 de 0.3010 est 0.6990 et nous calculerons a2 + a3 + 0.6690 - 1, ce qui revient au même mais est plus simple car nous avons bien la somme de 3 nombres positif, et retrancher 1 est une opération relativement simple.
La table devra alors mentionner 0.6690.
Convention d'écriture
On choisit le protocole suivant: on mentionnera dans la table 0.6990 précédé d'un 1 souligné ou barré ou surligné pour rappeler qu'il faudra retirer 1 au résultat, soit 1.6690. Comme je ne sais pas le faire avec le tableur, j'ai souligné tous les nombres qui impliqueront de retrancher 1 à la somme a1 + a2 + a3.
Faire apparaitre la valeur dans un tableur
Sur le plan mathématique, tout se passe comme ci l'équation était 2 - log(1-cosP). En effet 2 - 0.3010 = 1.6990.
C'est donc ce calcul qu'il faudra insérer dans le tableur excel pour 090 < LHA < 270, donc dans la partie gauche du tableau.
On remarque sur le graphe ci dessus que:
- la courbe rouge reste dans le dommaine positif
- pour un LHA donné, l'écart entre la courbe rouge et la droite passant par y = 2 est égal a l'écart entre la courbe bleue et la droite passant par 0. Et c'est cet écart qui représente a1.
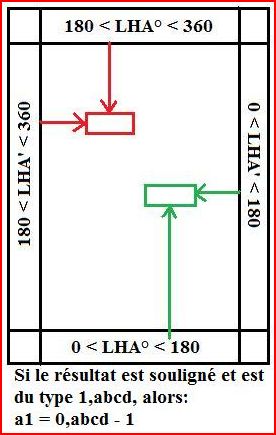
Utilisation de la Table
- pour 180 < LHA < 360
- lire les degrés sur la ligne du haut
- lire les minutes sur la colonne de gauche
- pour 0 < LHA < 180
- lire les degrés sur la ligne du bas
- lire les minutes sur la colonne de droite
- On lira le résultat a1dans la "case intercection" des degrés et minutes, à l'interieur du tableau, -Log(1 - cosLHA)
- SI le nombre est souligné, alors a1 = 0,abcd - 1