Table 2 pour trouver a2 = -Log(cosD) et a3 = -Log(cosL)
Cette table représente la fonction g(x) = -log(cosx). Elle permet de trouver -Log(cosD) et -Log(cosL) avec L et D variant entre -90(S) et 90(N). Or cos(x) = cos(-x). Il suffira d'avoir un tableau qui va de 0°à 90°.
- 0 < L < 90, donc cosL < 1, -Log(cosL) >0
- 0 < D < 90, donc cosD < 1, -Log(cosD) >0
a2 et a3 sont positifs et inférieur à 1
Habituellement, la table 2 est donnée pour des angles inférieurs a 75° car aucun astre n'a une Déclinaison de 75° et il est rare que l'on navigue au dessus ou en dessous de cette Latitude. Comme je ne suis pas à une page prés, j'ai fait le tableau jusque 90°, ce qui représente 6 pages au lieu de 5.
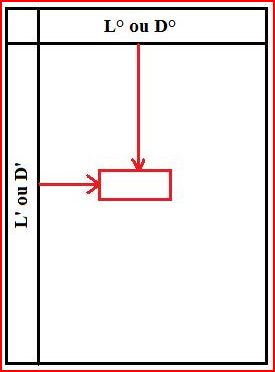
- Sur la ligne du haut on pourra lire les degrés de L ou de D
- Sur le côté on pourra lire les minutes de L ou de D
- On lira le résultat a2 ou a3 dans la "case intercection" des degrés et minutes, à l'interieur du tableau, -Log(cosD) ou -Log(cosL)
Table 3 pour trouver a4(a2 + a3 + a1)
Cette table représente la fonction h(x) = 10-x
avec x > 0, alors 10-x <1, donc a4 est de la forme 0,abcd avec ab < 99 et cd <99, ainsi a4 < 1. Nous aurons
- en abcisses (ligne du haut): ab de 1 en 1 avec 0 < ab <99 pour les dixièmes et centièmes
- en ordonnées (colonne de gauche): cd de 2 en 2 (la précision sera suffisante) avec 0 < cd < 99 pour les millièmes et dix millièmes.
Après avoir trouvé les valeurs de a2 = -Log(cosD), a3 = -Log(cosL), a1 = -Log(1-cosP), il faut les additionner.
- S1 = a2 + a3 + a1 ou
- S1 = a2 + a3 + (partie décimale de a1) - 1 si le nombre dans le Tableau 1 est souligné.
- a4 = h(S1)
On cherche dans le centre du tableau la valeur S1. et on détermine ab et cd pour trouver a4 = 0.abcd.
Pour construire la table, nous devrons partir de ab et de cd pour afficher Z.
Nous devons calculer 10-z en écrivant \(10^{-Z} = \frac{ab}{100} + \frac{cd}{10000}\)
\(\Rightarrow log10^{-Z} = log[ \frac{ab}{100} + \frac{cd}{10000}]\)
\(\Rightarrow -Z = log[ \frac{ab}{100} + \frac{cd}{10000}]\)
\(\Rightarrow Z = - log[ \frac{ab}{100} + \frac{cd}{10000}]\)
Ainsi, nous pouvons remplir notre tableau et l'utiliser.
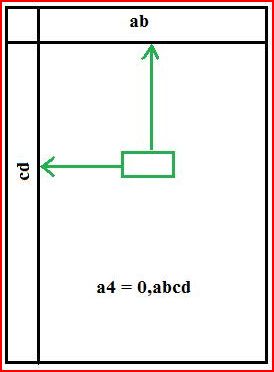
- Chercher la valeur S1 dans le milieu du tableau
- remonter vers le haut et trouver ab
- aller vers la gauche pour trouver cd
- a4 = 0.abcd
Pour finir, nous avons a4 = cosL cosD (1-cosLHA)
Table A pour trouver a5 et Hc
détermination de a5
Remarquons que cos(L - D) = cos(D - L)
Il s'agit de déterminer cos(L-D). Prenons plusieurs exemples:
- L = 50N = +50 et D = 20N = +20 alors L - D = 30
- L = 50S = +50 et D = 20S = -20 alors L - D = - 50 - (-20) = -30
- L = 50N = +50 et D = 20S = -20 alors L - D = 50 - (-20) = 70
- L = 50S = +50 et D = 20N = -20 alors L - D = - 50 - 20 = -70
alors on peut dire:
- si L et D sont de même nom (par exemple Nord) alors on les soustrait
- si L et D sont de nom contraire (l'un est Nord, l'autre est Sud) on les additione
Ainsi on se dispense d'utiliser les signes positifs ou négatifs de L ou D
Pour que l'astre soit observable, il faut que L-D soit inférieur à 90, sinon l'astre est sous l'horizon donc non mesurable.
De même, la hauteur de l'astre observé est toujours inférieure à 90°
Nous aurons donc besoin d'un tableau allant de 0 à 90°
Cette table représente la fonction i(x) = 1 - cosx
- Sur la ligne du haut on pourra lire les degrés de L - D
- Sur le côté gauche on pourra lire les minutes de L - D
- On lira le résultat a5 dans la "case intersection" des degrés et minutes la valeur a5
détermination de Hc
Il convient de calculer S2 = a5 + a4 = [1-cos(L-D)] + cosL x cosD x (1-cosP) et ce nombre est égal à [1- cos(90-Hc)]
On utilise encore 1 fois la table A pour trouver 90-Hc et en déduire Hc
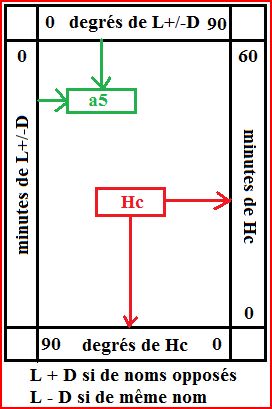
Comme cos(90-x) = sinx, la ligne du bas sera graduer en 90° - x et la colonne de droite en 60'-y.
- Chercher la valeur S2 dans le milieu du tableau
- dexcendre sur la ligne du bas et trouver les degrés de Hc
- aller dans la colonne de droite et trouver les minute de Hc