La majorité des cartes que vous utilisez sont des cartes Mercator Direct. Ce canevas est loxodromique. Dans ce chapitre, nous allons expliciter mathématiquement ce qu'est une loxodromie. Cela nous permettra de comprendre comment est construit un canevas loxodromique comme le canevas Mercator Direct, qui est trés utilisé pour les cartes marines. Les points suivants seront vus:
- Définition de la loxodromie
- Les formules de l'estime qui permettent d'introduire les notions suivantes:
- la latitude croissante Lc
- la route
- la distance
- Les formules approchées de l'estime
- Un exemple de calcul de route loxodromique
- Comment déterminer l'angle de route Rv
Définition de la loxodromie

Parmi l'infinité de routes qui joignent 2 points quelconques de la Terre, il en est une particulière: celle qui coupe tous les méridiens sous un même angle: c'est la loxodromie.
Entre 2 points, il existe une infinité de loxodromies. La seule qui nous intéresse est la plus courte, c'est à dire celle qui fait moins d'un demi tour de la Terre.
\[Route fond = constante \Rightarrow Loxodromie\]
La loxodromie entre 2 points A et B est donc définie par l'angle constant sous lequel elle coupe tous les méridiens. Cette angle est appelé angle de route: Rv
La distance loxodromique m est la distance parcourue entre A et B en suivant la loxodromie.
On peut calculer simplement Rv et m entre 2 points A et B de coordonnées géographiques connues au prix de quelques approximations, en utilisant les formules de l'estime.
Quelques loxodromies particulières:
- les méridiens: Rv = 000 ou Rv = 180 et m = ΔL (en minute)
- les parallèles: Rv = 090 ou Rv = 270 et m = Δg x cos Lm (voir le chapitre "mesurer une distance")
Les formules de l'estime
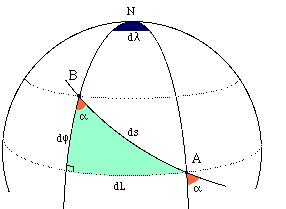 Soit AB la loxodromie joignant:
Soit AB la loxodromie joignant:
- A de longitude LA et de latitude ΦA: A (LA,ΦA),
- B (LB,ΦB) et
- α ( < à 90°) l'angle sous lequel cette loxodromie coupe les méridiens.
Considérons maintenant 2 méridiens infiniment voisins, écartés en longitude de dg, alors le triangle AB(Angledroit) peut être considéré comme plan. Et:
- ds, la distance loxodromique entre a et b (2 points de cette mini loxo) est infiniment petite
- dL, écart de longitude infiniment petit dL = dg x cosφ
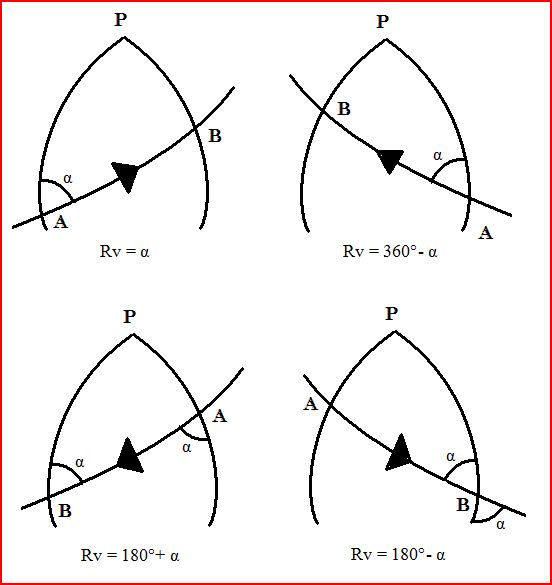
Calculons l 'angle α pour trouver l'angle de route Rv = 360-α
Alors, \(tan\alpha = \frac{dL}{dφ} = \frac{dg\times cosφ}{dφ}\)
\(\Rightarrow dg= tan\alpha \times \frac{dφ}{cosφ}\)
La loxo AB est composée d'une somme de petits éléments ab. En ajoutant tous ces petits éléments, il vient:
\(L_B-L_A = dλ = \int_{A}^B dg = \int_{A}^B tan\alpha \times \frac{dφ}{cosφ}\)
\(= tan\alpha \times \int_{A}^B \frac{dφ}{cosφ}\) car α=constant
On démontre que \( \int \frac{dφ}{cosφ} = log \vert tan(\frac{Φ}{2}+\frac{π}{4}) \vert\). Cette quantité est appelée latitude croissante: Lc
\(L_B-L_A = dλ = tan\alpha \times (Lc_B-Lc_A) = tan\alpha \times ΔLc\)
Il vient donc la 1ère formule de l'estime permet de trouver l'angle α et trouver l'angle de route Rv = 360°-α
\[\boxed{tan\alpha = \frac{dλ}{ΔLc}}\]
avec \(Lc = log \vert tan(\frac{Φ}{2}+\frac{π}{4}) \vert\)
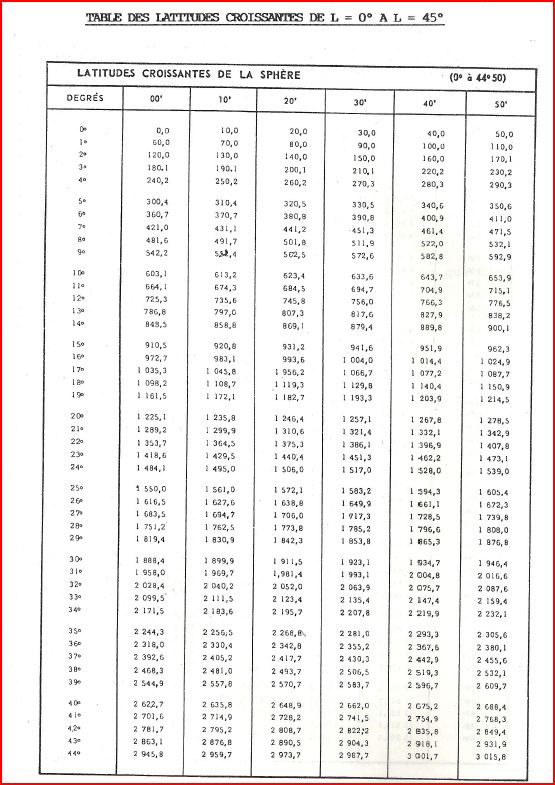
Cette expression Lc a été précalculée et figure dans des tables pour toutes les latitudes de 0° à 90°. La latitude croissante est un angle, mais sur les tables elle est donnée en minutes d'angle. On peut aussi la calculer avec une calculette.
On en déduit la route constante Rv = 360-α dans le cas du tracé ci dessus servant à la démonstration.
Voici le tableau des latitudes croissantes pour des latitudes allant de 00° à 45°
Calculons la distance loxodromique m
 Dans le triangle plan infiniment petit , on peut écrire \(ds = \frac{dφ}{cosα}\)
Dans le triangle plan infiniment petit , on peut écrire \(ds = \frac{dφ}{cosα}\)
\(m = \int_{A}^B ds = \int_{A}^B \frac{dφ}{cosα} = \frac{1}{cosα} \int_{A}^B dφ = \frac{Φ_B -Φ_A}{cosα}\)
La 2ème formule de l'estime permet de trouver la distance loxomdromique
\[\boxed{m = \frac{ΔΦ}{cosα}}\]
Les formules approchées de l'estime
Si on pose Φm comme la latitude moyenne entre A et B, \( Φ_m = \frac{Φ_B +Φ_A }{2}\), alors on peut démontrer que:
\(ΔLc = \frac{ΔΦ}{cosΦ_m}\)
si \(tan\alpha = \frac{dλ}{ΔLc}\) alors
\[\boxed{tan\alpha = \frac{dλ \times cosΦ_m}{ΔΦ}}\]
Exemple de calcul
A (N20°,E010°), B(N25°,E015°), calculer la route entre A et B ainsi que la distance AB
Calcul de α (1ère formule de l'estime)
\(tan\alpha = \frac{dλ}{ΔLc}\) avec
dλ =E015 - E010 = 5° = 300'
ΔLc = LcB-LcA = Lc25-Lc20 = 1550'-1225.1' = 324.9'
\(tan\alpha = \frac{300}{324.9} = 0.923\)
ce qui donne α=42,7° = Rv
Calcule de m (2ème formule de l'estime)
\(m = \frac{ΔΦ}{cosα} = \frac{N25-N20}{cos42,7} = \frac{300'}{0,734} = 428 MN\)
Avec la formule approchée:
\(tan\alpha = \frac{dλ \times cosΦ_m}{ΔΦ} = \frac{ 300 \times cos22.5}{300} = 0,923\)
α=42,7° = Rv
Détermination de Rv
Une fois déterminé α, il faut calculer l'angle de route Rv, entre le Nord et l'axe de la route: