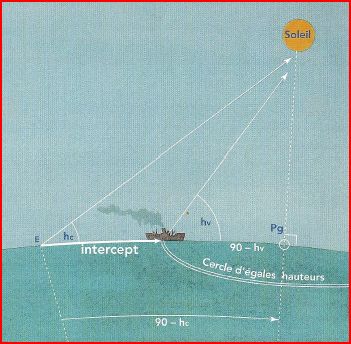
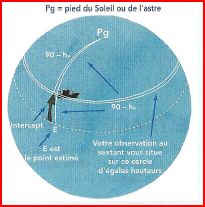
L'intercept
L'intercept est la distance entre les 2 cercles de position ayant pour Hauteur Hv et Hc (et pour rayon respectifs Rc et Rv), le long de l'axe Zc
Nous connaissons maintenant:
- Notre position estimée E
- g= 003°00'W
- L = 47°30'N
- Zc = 217°
- Hc = 13°10'45"
- Hv = 13°10'48"
On peut alors calculer l'intercept
Intercept = Hv-Hc = +3'
Tracer la droite de hauteur
Nous allons définir un repère dont le centre est le point estimé E (ce point peut aussi être appelé point déterminatif)
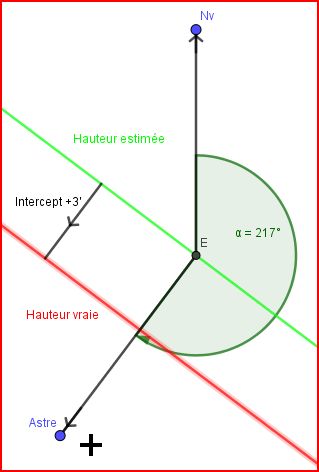
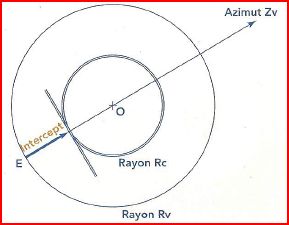
Depuis E, on trace l'Azimut Zc avec la règle Cras. Cet azimut est la direction du pied de l'astre sur la sphère terrestre. Cette azimuth est orienté: le signe positif vers l'astre.
Alors la droite de hauteur estimée est perpendiculaire à Zc et passe par E
Et la droite de hauteur vraie, notre position vraie est décalée de +3' = 3MN par rapport à la droite de hauteur estimée.
Notre bateau se situe sur quelque part sur la droite de hauteur vraie.
Pour déterminer notre position, il faudra
- construire une deuxime droite de hauteur, avec un autre astre, ou
- recommencer plus tard et faire un transfert de lieu de position (comme un transfert d'amer)
Ainsi nous aurons 2 droites de position sécantes et notre position sera à l'intersection de ces 2 droites.
Notre position est sur la droite de hauteur rouge.
2 représentations graphiques de la droite de hauteur
Afin de bien comprendre ce que nous avons fait, voici 2 dessins:
Importance de la précision du point estimé E
- L'intercept est de nature différentielle. Ne pouvant se situer directement par rapport au pied de l'astre, on se situe en terme d'écart par rapport à un point connu: E le point estimé (ou point arbitraire)
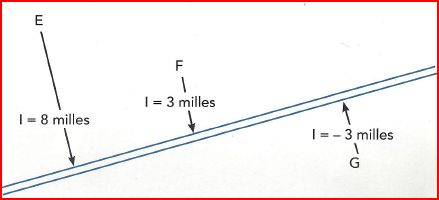
- La construction de la droite de hauteur est indépendante du point E choisi comme le montre la figure suivante:
Les droites de hauteur construites à partir des points E, F, G, sont confondues avec celle établie à partir de E
La position du point estimé qui sert à calculer Hc n'est pas importante. En fonction de la précision de l'estimée, seul l'intercept sera plus ou moins important. Mais la droite de hauteur vraie, elle, sera finalement toujours au même endroit.
On s'attachera à choisir un point dont les coordonnées sont faciles à utiliser et avec des valeurs arrondies.