Cette règle permet de calculer de tête, approximativement et rapidement la hauteur d'eau à un moment donné, en connaissant l'heure de BM ou de PM et le marnage.
Elle permet aussi de tracer le graphe des 12èmes qui permet de trouver graphiquement et plus précisément la hauteur d'eau.
La formule harmonique décrivant la marée est du type: \[hauteur = Z_0+cos(ωt+φ)\]
Autrement dit, la courbe décrivant la marée est une sinusoïde.
A l'échelle d'une marée, on peut considérer que le coefficient de marée est constant.
La marée varie de PM à BM dans un temps de 6 "heures marées".
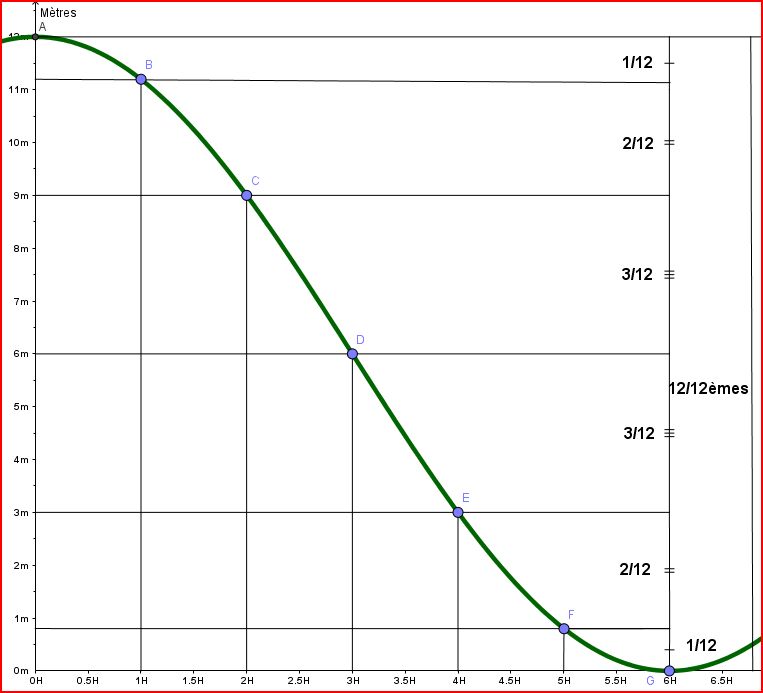
Etudions les hauteurs d'eau à chaque "heure marée" en considérant un marnage de 12 mètres.
On remarque que:
- la 1ère heure marée, l'eau baisse de 1 m, soit 1/12ème du marnage
- la 2ème heure marée, l'eau baisse de 2 m, soit de 2/12ème du marnage
- la 3ème heure marée, l'eau baisse de 3 m, soit de 3/12ème du marnage
- la 4ème heure marée, l'eau baisse de 3 m, soit 3/12ème du marnage
- la 5ème heure marée, l'eau baisse de 2 m, soit de 2/12ème du marnage
- la 6ème heure marée, l'eau baisse de 1 m, soit de 1/12ème du marnage
En 6 heures marée, l'eau baisse de 12 m, soit 12/12ème du marnage.
Lors de la 1ère et de la dernière heure marée, la variation d'eau est légèrement inférieure à 1/12ème. On remarque au point F que la hauteur d'eau est inférieure à 1/12ème. Il conviendra de prendre un pied de pilote assez conséquent, de l'ordre de 50 cm au moins.
On peut retenir la suite de nombre 1, 2, 3, 3, 2, 1 correspondant au nombre de 12ème à chaque heure marée
Voici ce que dit le BMA2017:
La règle des Quarts
Cette règle découle directement de la règle des 12èmes.
L'eau baisse d'1/4 du marnage:
- les 2 premières heures
- la 3ème heure
- la 4ème heure
- les 2 dernières heures
Ces 2 règles permettent de faire un calcul approximatif et rapide de la hauteur d'eau à un moment donné