D'où vient la force de Coriolis?
Les lois de la mécanique classique ont une forme assez simple dans des repères absolus (Galiléens, Coperniciens) qui sont des axes passant par des étoiles fixes.
Le mouvement des particules atmosphériques est repéré en pratique au moyen d'instruments qui sont liés à la surface de la terre. Or, la surface de la Terre ne constitue pas un repère fixe (et oui !! elle tourne!!). Et l'étude du mouvement des particules par rapport à un système de référence lié à la Terre introduit des forces fictives dites forces d'inertie, au côté des "forces vraies".
Ces forces fictives, alors qu'elles peuvent être considérées comme négligeables dans certains cas, ne le sont plus dans le cas de la physique atmosphérique car elles sont du même ordre de grandeur que les forces vraies. (par exemple, la masse d'une bulle d'air est du même ordre de grandeur que la force due aux variatiions de pression).
Nous allons dans un premier temps déterminer \(\overrightarrow{V_a(M)}\), la vitesse absolue d'un point M, c 'est à dire la vitesse de M par rapport au repère galiléen OXYZ.
Puis nous déterminerons \(\overrightarrow{\Gamma_a(M)}\), l'accélération absolue de M par rapport a OXYZ.
Ainsi nous mettrons en évidence l'accélération de Coriolis \(2\overrightarrow{\Omega} \wedge \overrightarrow{V_r(M)}\), la force de Coriolis \(-2m \overrightarrow{\Omega} \wedge \overrightarrow{V_r(M)}\), et nous expliquerons l'effet de la force de Coriolis sur un petit volume d'air en déplacement.
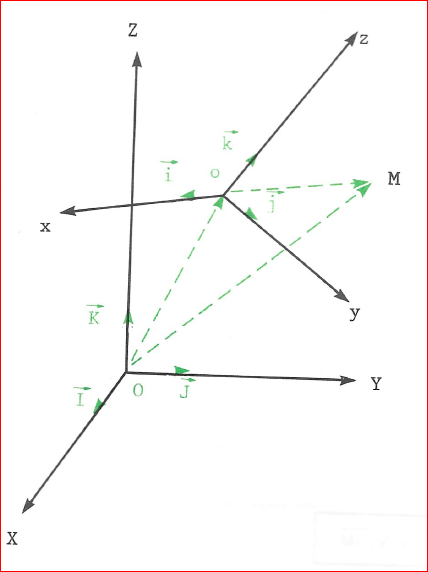
Préliminaires: position d'un point M
Soient:
- le repère O, X, Y, Z, (lettres majuscules) système de référence absolue rigoureusement immobile
- dont les vecteurs unitaires sont \(\overrightarrow{I}\), \(\overrightarrow{J}\), \(\overrightarrow{K}\)
- le repère o, x, y, z, (lettres minuscules) système de référence relatif lié à la terre, qui se déplace en conséquence par rapport au premier repère OXYZ
- dont les vecteurs unitaires sont \(\overrightarrow{i}\), \(\overrightarrow{j}\), \(\overrightarrow{k}\)
- un mobile (une molécule d'air par exemple) matérialisé par un point M, qui se déplace par rapport à ces 2 systèmes
Alors:
- les coordonnées du point M dans le système de référence relatif sont x, y, z, et le vecteur \(\overrightarrow{oM}\) sera noté: \[\overrightarrow{oM} = x \overrightarrow{i} + y \overrightarrow{j} + z \overrightarrow{k}\]
- les coordonnées du point M dans le système de référence absolu sont X, Y, Z, et le vecteur \(\overrightarrow{OM}\) sera noté: \[\overrightarrow{OM} = X \overrightarrow{I} + Y \overrightarrow{J} + Z \overrightarrow{K}\]
On pourra alors écrire: \[\overrightarrow{OM} =\overrightarrow{Oo}+\overrightarrow{oM} \]
