La projection Mercator

La projection Mercator Directe est une projection cylindrique, tangente à l'équateur du globe terrestre. Elle a été formalisée par le géographe flamand Gerardus Mercator en 1569. Elle s'est imposée comme le planisphère standard dans le monde grâce à sa précision pour les voyages marins.

Dans ce chapitre, nous allons voir:

• Comment est construit le canevas Mercator Direct
• L'étude de l'Echelle et de la conformité du canevas
• La construction graphique d'un canevas Mercator Direct
• les défauts de la projection Mercator

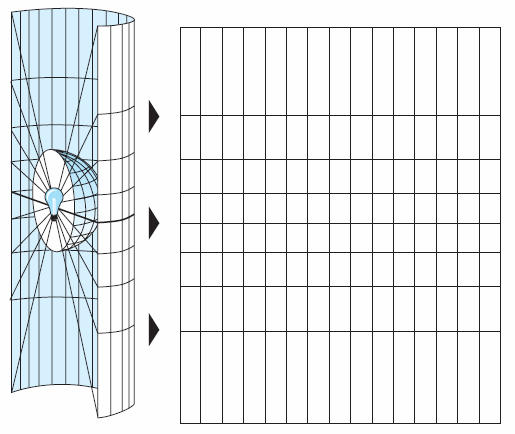
Le canevas est construit à partir d'une projection géométrique, depuis le centre de la sphère réduite, sur un cylindre tangent à cette sphère à l'équateur.

Une telle projection donne l'allure du canevas suivante:

• les méridiens: droites verticales, parallèles entre elles, régulièrement espacées. Ces droites sont équidistantes. 2 méridiens séparés par la même différence de longitude g auront toujours le même écartement sur le canevas.
• les parallèles: droites perpendiculaires au méridiens, donc droites horizontales, parallèles entre elles , mais non régulièrement espacées. La distance d'un parallèle de latitude L à l'équateur est égale à la Latitude croissante Lc de ce parallèle. Lc est exprimée en minute d'angle

Construction de la carte

Une carte ne peut pas être équidistante sur toute sa surface. Il est donc impossible de fixer l'échelle de la carte. Par contre, une carte peut être considérée comme équidistante sur une petite portion. On peut donc fixer, par exemple, l'échelle à l'équateur E_0.

\(E_0=\frac{ab^{mm}}{AB^{mm}}\)  et   \(U_0 = \frac{ab^{mm}}{AB^{MN}}\)

donc \( U_0 = E_0 \times 1.852 \times 10^6\)

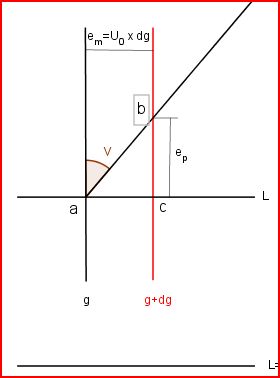
Le canevas est cylindrique. On peut commencer à tracer un méridien de longitude g, et un parallèle de latitude L.

Essayons de placer le méridien de longitude g+dg (dg exprimé en minutes)

Ecart entre 2 méridiens: e_m=U₀ x dg' (en minute donc en MN)

Plaçons maintenant le parallèle de latitude L+dL

Il faut déterminer à quelle distance e_p, exprimée en mm, se trouve ce parallèle du parallèle de latitude L.

soient 3 points A, B, et C (C= l'angle droit sur la Terre) et leur image a, b, c sur la carte. Les coordonnées de A, B, C sont les suivantes:

• A (L,g)
• B (L+dL, g+dg)
• C (L, g+dg) (l'angle droit)

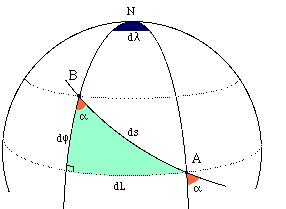
sur la Terre, la loxo AB fait un angle α tel que \(tanα = \frac{dg}{dLc}\)     (1)

La carte devant être loxodromique et conforme, la droite ab sur la carte doit couper les méridiens sous le même angle α que sur la Terre.

Or sur la carte \( tanα = tanV= \frac{U_0 \times dg}{e_p} \)     (2)

(1) = (2) \(\Rightarrow \frac{dg}{dLc} = \frac{U_0 \times dg}{e_p}\)

il vient alors: \(e_p = U_o \times dLc\)

Etude de l'échelle et de la conformité

Nous allons vérifier que notre carte est bien conforme. Pour cela nous allons calculer l'échelle autour d'un point et vérifier que cette valeur est bien la même suivant 2 directions perpendiculaires: le long d'un méridien et d'un parallèle.

Soient 3 points A B C sur la Terre et leur image sur la carte a b c

• A (L,g)
• B (L+dL, g+dg)
• C (L, g+dg)

Echelle suivant le parallèle Ep

\(E_p = \frac{ac}{AC} = \frac{U_0 \times dg}{dg \times cosL \times 1.852 \times 10^6} = k \times \frac{1}{cosL}\)

avec \(k=\frac{U_0}{1.852 \times 10^6}\)

Echelle suivant le méridien Em

\(E_m = \frac{bc}{BC} = \frac{U_0 \times dLc}{dL \times 1.852 \times 10^6}\)

or \(dLc= \frac{dL}{cosL}\)

ce qui abouti à : \(Em = k \times \frac{1}{cosL}\)

\[\boxed {Ep = Em,\Rightarrow \space canevas \space conforme}\]

Par ailleurs, on peut remarquer que à la latitude L:

\(E_L = \frac{ E_0}{cosL}\) et   \(U_L = \frac{U_0}{cosL}\)

avec E₀ et U₀ les echelle et unité à la latitude 0, donc à l'équateur.

 :

Construction graphique d'un canevas Mercator

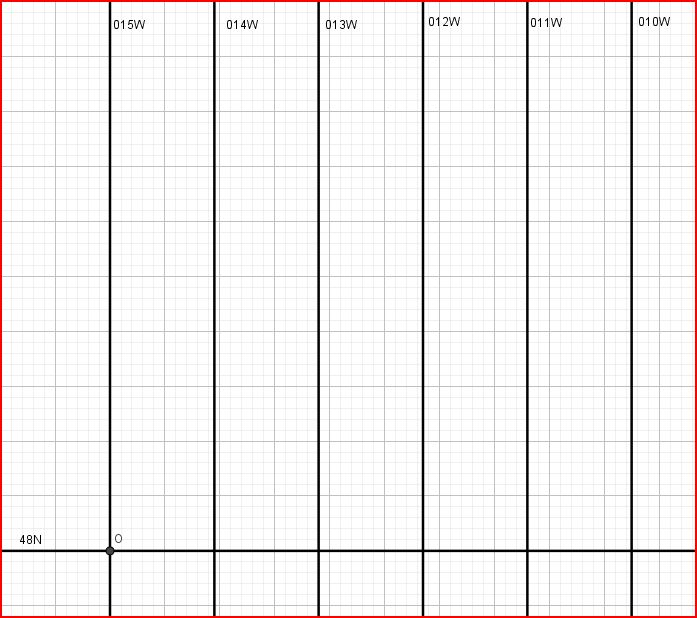
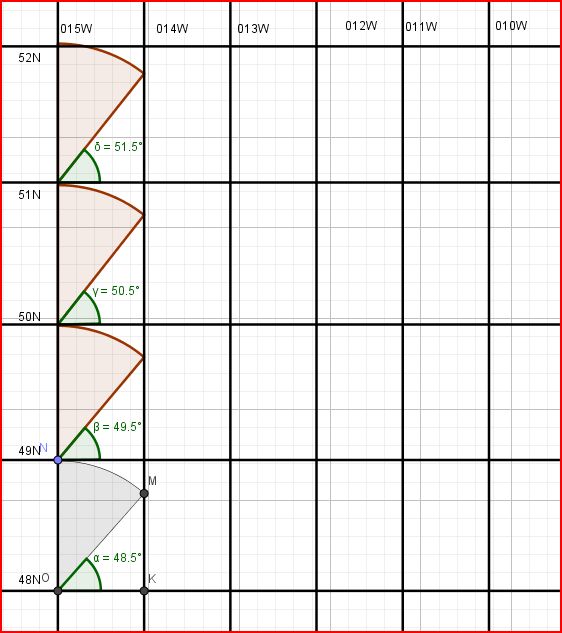
Nous voulons construire un canevas Mercator entre les méridiens 015W et 010W, et les latitudes 48N et 52N.

On souhaite que ce sur ce canevas, 1mm = 2NM à la Latitude moyenne. (je vous rappelle que le canevas n'est pas équidistant et que par conséquent, il n'existe pas d'échelle rigoureusement constante, d'ou la nécessité de préciser à quelle latitude l'Echelle ou l'Unité ont cette valeur),

L'Echelle de cette carte est trés grande pour une carte marine côtière. Mais ce qui est important, c'est de comprendre ce qui se passe..........

On peut commencer par tracer le méridien 015W et la latitude 48N, 2 droites perpendiculaires

Plaçons ensuite les méridiens: 

• Latitude moyenne = 50N
• U₅₀ = 1mm/2NM = 0.5
• U₀ = U_L x cosL_m = 0,5 x cos50 = 0,321 mm/MN à l'équateur
• e_m = U₀ x dg' = 0.321 x 60' #19 mm

Les méridiens seront espacés de 19 mm

Plaçons maintenant les parallèles

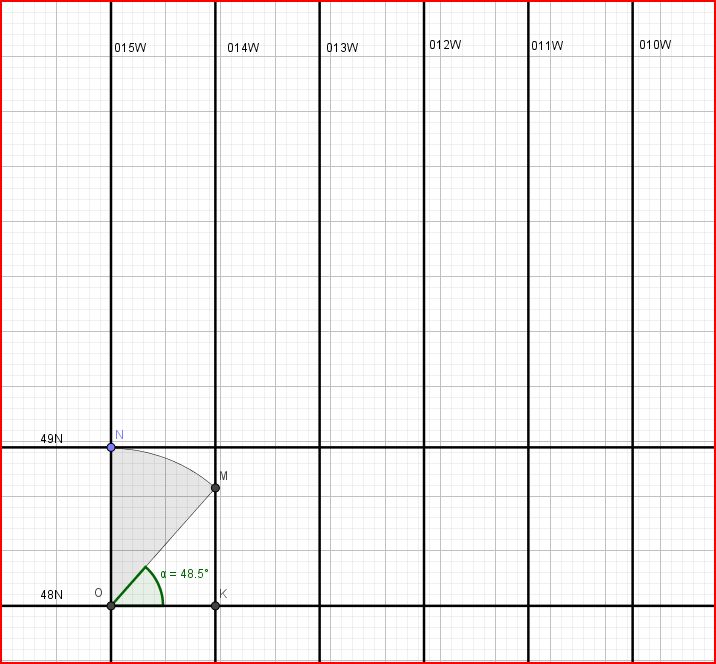
pour placer le parallèle 49N,

• tracer un angle de 48,5° (latitude moyenne entre 48N et 49N) qui vient couper le méridien suivant en M
• rabattre le point M à l'aide d'un compas sur le méridien 015W (point N)
• Le parallèle 49N passe par le point N

• recommencer le processus pour les parallèles 50N 51N 52N

Remarque: \(OM = \frac{OK}{cos48,5} = \frac{60 U_0}{cos L_m} = U_0 \times dLc = U_0 \times (Lc_{49}-Lc_{48})\)

Et c'est bien le principe de Mercator

Les défauts de la projection Mercator

Les cartes traditionnelles inspirées des travaux de Mercator destinés à la navigation ont pour principal défaut de donner une idée erronée des surfaces occupées par les différentes régions du monde, et donc des rapports entre les peuples. 

Ainsi :

• L’Amérique du Sud semble plus petite que le Groenland ; en réalité, elle est huit fois plus grande : 17,84 millions de kilomètres carrés contre 2,16 millions.
• L’Inde (3,3 millions de kilomètres carrés) semble de taille identique à la Scandinavie (1,1 million de kilomètres carrés).
• L’Europe (9,7 millions de kilomètres carrés) semble plus étendue que l’Amérique du Sud, pourtant près de deux fois plus grande (17,8 millions de kilomètres carrés).
• La Russie (17 millions de kilomètres carrés) semble beaucoup plus étendue que l'Afrique (30 millions de kilomètres carrés) alors que cette dernière est plus grande que l'Inde, la Chine, les États-Unis, l'Europe et le Japon réunis.
• L'Alaska apparaît aussi grand que le Brésil qui est pourtant 5 fois plus étendu.
• L'Antarctique apparaît comme le plus grand continent, alors qu'il n'est en réalité que le 5^ème par sa superficie.
• L'Afrique apparaît de taille équivalente au Groenland alors qu'elle est de 14 à 15 fois plus étendue

Le canevas Mercator, si il est conforme, et est pratiquement équidistant, n'est pas équivalent . C'est à dire qu'il ne conserve pas les rapports de surfaces constants.

Pour pallier ces déformations, Arno Peters proposa une projection cylindrique (comme celle de Mercator) qui préserve les superficies relatives : la projection de Peters. Elle perd en revanche le caractère conforme, c'est-à-dire qu'elle ne préserve pas les angles et donc la forme des continents. Cette projection utile pour les géo politiciens n'a aucun intérêt pour la navigation.