En 1687, Newton publie La Théorie de la Gravitation ou de l'Attraction Universelle. C'est la première explication plausible de l'origine de la marée.
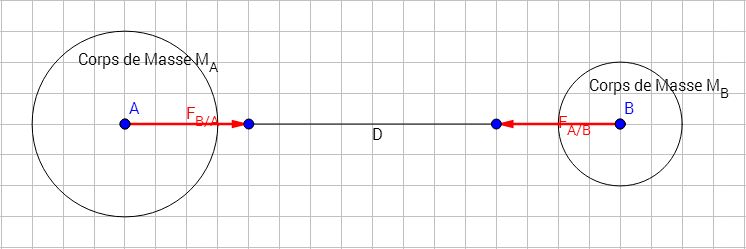
Deux corps ponctuels de masses respectives MA et MB, séparés d'une distance D, s'attirent avec des forces de mêmes valeurs (mais vectoriellement opposées). Ainsi:
\[ F_{(A/B)}=F_{(B/A)}=G×\frac{(M_A×M_B)}{D^2}\]
- \(M_A\) et \(M_B\): les masses des 2 corps A et B en Kg
- \(D\): la distance entre les 2 corps en m (mètres)
- \(G\): la constante gravitationnelle de Cavendish = 6.67x10-11 N.m2 . Kg-2
On comprend dès lors que:
- La Lune a une influence sur la marée car elle est très proche de la Terre, donc le diviseur \(D^2\) devient petit
- Le Soleil a une influence sur la marée car sa masse est très grande
- Les autres astres et planètes, étant données leurs masses et leurs distances à la terre, ont une influence négligeable.
| Masse (Kgs) | Distance (m) | F pour 1000Kg d'eau (N) | |
| Lune | 7.4x1022 | 3.8x108 | 3.4x10-2 |
| Soleil | 2x1030 | 1.5x1011 | 5.9 |
| Terre | 6x1024 |
On remarque que dans ces conditions, la marée est principalement due au soleil. Ce qui ne correspond pas aux observations. En effet, la hauteur de la marée varie en fonction des phases de la Lune.
La marée d'un Astre:
Pour avoir une meilleure idée de la force totale subie, il faut ramener les forces exercées par rapport au centre de la Terre. Dans ce cas, la force subie par une masse de 1kg d'eau est inversement proportionnel au cube de la distance Terre/Lune ou Terre/Soleil.
Considérons une Masse de 1 Kg d'eau située à différents endroits de la Terre, quelle force cette masse d'eau subirait elle de la part de la Lune? Appliquons la loi de la gravitation à cette masse de 1Kg d'eau qui serait située en différents endroits du globe terrestre avec les données suivantes:
- MA = M = masse de la Lune
- MB = 1 = masse de 1Kg d'eau
- G = 6.67x10-11 = constante de Cavendish
Alors, vu au niveau du "cosmos", nous aurions:
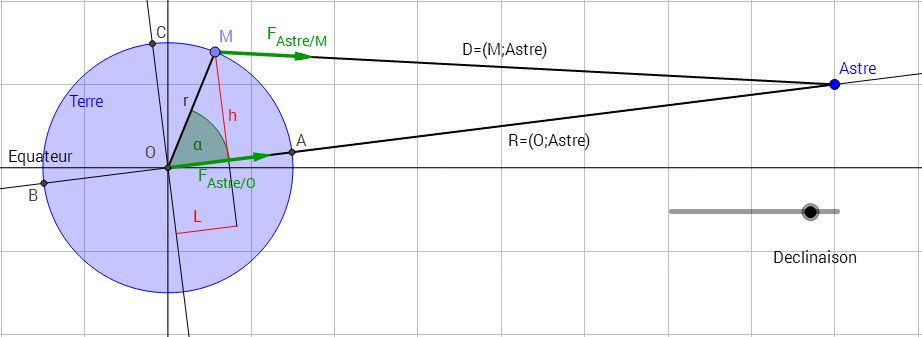
\(F_O= \frac{G×M}{R^2} \) et \(F_M=\frac{G×M}{D^2}\)
avec Pythagore et un peu de trigonométrie:
- \(D^2=(R-L)^2+h^2\)
- \(h=rsinα\)
- \(L=rcosα\)
Donc:
\(D^2=(R-rcosα)^2+(rsinα)^2\)
\(D^2=R^2-2Rrcosα+r^2cos^2α+r^2sin^2α\)
\(D^2=R^2-2Rrcosα+r^2(cos^2α+sin^2α)\)
\(D^2=R^2-2Rrcosα+r^2\)
Ce qui donne : \(F_O=\frac{G×M}{R^2}\) et \(F_M=\frac{G×M}{R^2-2Rrcosα+r^2}\)
Remettons tout cela dans le repère Terrestre en calculant \(F_M- F_O\) :
\(F_M- F_O= \frac{G×M}{R^2-2Rrcosα+r^2} - \frac{G×M}{R^2}\)
\(F_M- F_O=GM (\frac{R^2-(R^2-2Rrcosα+r^2)}{R^2(R^2-2Rrcosα+r^2)})\)
\(F_M- F_O=GM (\frac{2Rrcosα-r^2}{R^4-2R^3rcosα+R^2r^2})\) avec r << R (1)
\(F_M- F_O=GM(\frac{2Rrcosα}{R^4})=GM(\frac{2rcosα}{R^3})\) (2)
Appelons cette force \(f_M\) : \(f_M=F_M- F_O= GM(\frac{2rcosα}{R^3})\)
On remarque grâce aux résultats (1) et (2) que \(f_M\):
- est proportionnelle à la masse de l'Astre
- est inversement proportionnel au cube de la distance de l'Astre
- est minimum pour α=90° ou 270° (l'Astre est à l'horizon, NADIR)
- ne s'annule jamais (\(F_{Astre/M}\) ne peut jamais être égal à \(F_{Astre/O}\) en force et en direction en même temps)
- est maximum en A et B (l'Astre passe dans le plan méridien de l'observateur, ZENITH)
Cherchons les valeurs en différents points du globe:
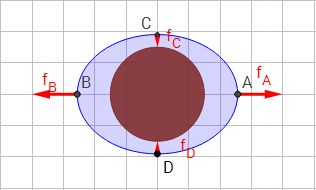
- en A: \( α=0\), \(cosα=1\), en conséquence, \(f_A=GM(\frac{2r}{R^3}) = f\)
- en B: \( α=π\), \( cosα=-1\), en conséquence, \(f_B=GM(\frac{-2r}{R^3}) = -f\)
- en C: \( α=π/2\), \( cosα=0\), en conséquence, \(f_C = \frac{-r^2}{R^4}\) soit une force très faible et dirigée vers le bas.
\(f_A\) et \(f_B\) sont des forces opposées. Ce qui signifie que l'eau est attirée du côté de la Lune (\(f_A\)) et que tout se passe comme si l'eau était repoussée du côté de la Terre opposé à la Lune (\(f_B\)). Ces forces sont dans l'axe Terre-Astre. On peut dire qu'elles étirent la masse d'eau.
\(f_C\) et \(f_D\) sont aussi opposées. Elles ne s'annulent jamais, et on peut dire qu'elles compressent la masse d'eau.
| Masse (Kgs) | Distance (m) | f pour 1000Kg d'eau (N) | |
| Lune | 7.4x1022 | 3.8x108 | 1.1 10-3 |
| Soleil | 2x1030 | 1.5x1011 | 5 10-4 |
| Terre | Rayon r = 6.371x106 m |
On s'aperçoit alors que:
- FLune/Terre = 2.2 x FSoleil/Terre
- La force exercée par la Lune est environ 2 fois plus forte que la force exercée par le Soleil
- la force gravitationnelle dépend de α, donc de la déclinaison de l'Astre et de la position de M