Les tables de Bataille permettent de trouver Zc. Pour cela, 2 solutions existent:
- je connais l'heure, donc P, D, L et j'utilise la formule des 4 éléments consécutifs
- je connais l'heure et Hc (utilisation des Table de Dieumegard) et j'utilise l'analogie des Sinus.
1ere Methode
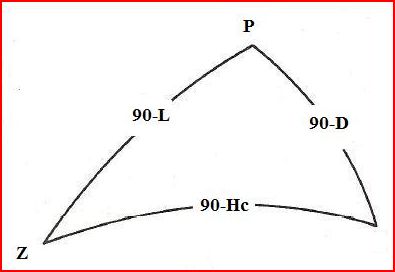
Cette méthode considère que l'on connait uniquement l'heure et notre position estimée, soient P, L, D. Le 4ème élément est alors Z
Bataille a écrit la formule des 4 éléments consécutifs sous une autre forme. Cette nouvelle forme va permettre de rentrer dans des tables précalculées afin de nous rendre le calcul plus facile.
La formule des 4 éléments consécutifs nous dit: Ce Si cotés = Ce Si angles + Cosi Cosi
\(\Rightarrow\) cotan(90-D) sin(90-L) = cotanZ sinP + cos(90-L) cosP
\(\Rightarrow\) cotanZ sinP = cotan(90-D) sin(90-L) - cos(90-L) cosP
\(\Rightarrow\) tan(90-Z) sinP = tanD cosL - sinL cosP
\(\Rightarrow\) tan(90-Z) cos(90-P) = tanD cosL - sinL cosP
\[\Rightarrow \boxed{tan(90- Z) cos(90-P) = - cosP sinL + tanD cosL}\]
- table 1 : f(x;y) = cosx siny
- table 2 : g(x;y) = tanx cosy
Alors on peut écrire : \[\boxed{g(90-Z ; 90-P) = -f(P;L) + g(D;L) = m+n}\]
avec
- m = cosP sinL et
- n = tanD cosL
2eme méthode
Cette méthode considère que l'on connait la Hc, l'heure et notre position estimée, soient Hv, P, L, D.
L'analogie des sinus donne:
\(\frac{sinP}{sin(90-Hv)}=\frac{sinZ}{sin(90-D)}\)
ou encore:
\[\boxed{cosD \times sinP = cosHv \times sinZ}\]
- table 1 : f(x;y) = cosx siny
Alors on peut écrire : \[\boxed{f(D ; P) = f(Hv ; Z) = m}\]
avec
- m = -cosD sinP et
- m = -cosHv sinZ
Les tables de Bataille seront au nombre de 2:
- Table 1 : f(x ; y) = sinx cosy
- Table 2 : g(x ; y) = tanx cosy