Le canevas Stéréopolaire

Le canevas stéréographique polaire est un des plus vieux canevas à avoir été employés. Son utilisation remonte à l'antiquité grecque.

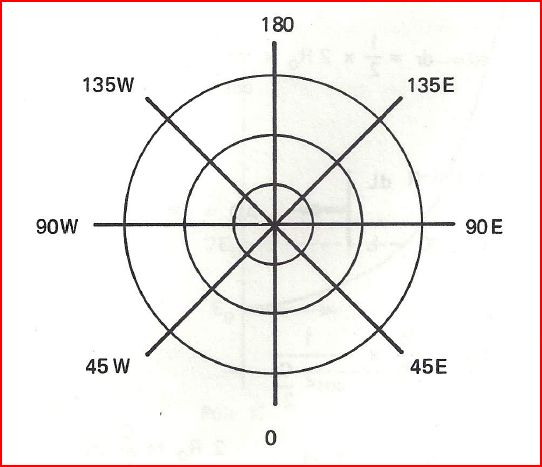
Ce canevas est utilisé pour les cartes météorologiques. C'est le standard international.

Il peut être utile pour les navigations dans les trés hautes latitudes.

Etude du canevas

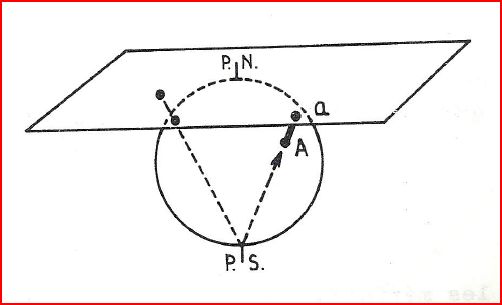
Le canevas est obtenu à partir d'une projection géométrique de tout point de la Terre sur un plan tangent, depuis le point opposé au plan tangent.

Pour obtenir un canevas stéréographique polaire, le plan tangent retenu est le plan tangeant à la sphère réduite au pôle Nord.

La projection sur ce plan de tous les points de la Terre sera faite à partir du Pôle Sud.

La sphère réduite est la petite sphère de rayon r_T, réduction directe de la Terre assimilée à une sphrede rayon r_T . 

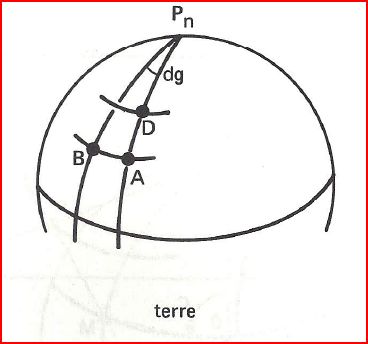
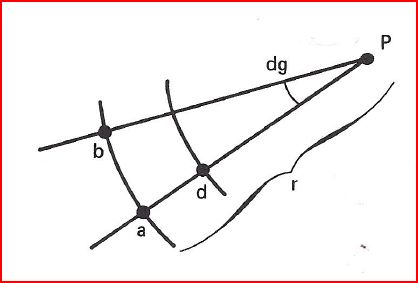
• Les méridiens seront des droites concourantes au pôle de tangence. L'angle dα sur la carte entre 2 méridiens séparés de par un écart de longitude dg sera: \[\boxed{dα = dg}\]
• Les parallèles seront des cercles concentriques, centrés sur le Pôle de tangence

Déterminons le rayon r d'un cercle représentant un parallèle de latitude L:

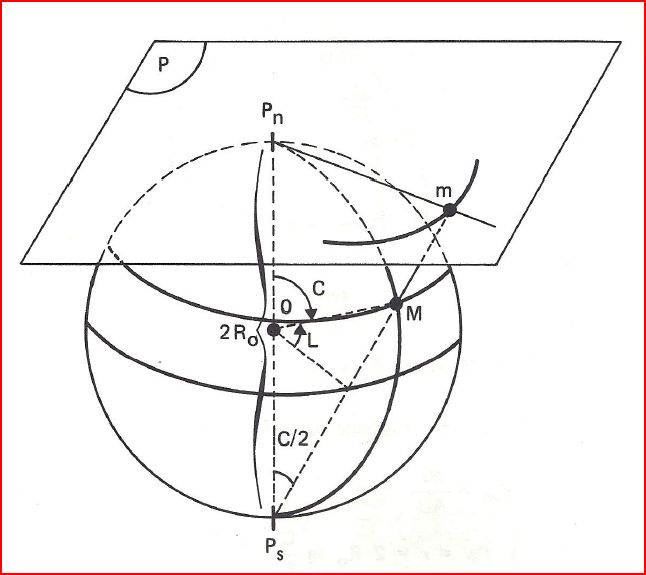
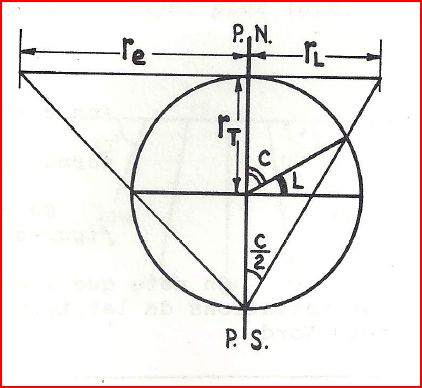
Si M est de latitude L, alors M est de colatitude C

Si P_NOM  = C alors P_NP_SM = C/2

\(P_Nm =   P_NP_S \times tan\frac{C}{2}\)

avec P_Nm = r et P_NP_S = 2 x R₀

donc (0)  \(\boxed{r = 2R_0tan(\frac{C}{2})}\)

Etude de la conformité

Pour que le canevas soit conforme, il faut et il suffit que E_M = E_P

Soient 3 points  sur la Terre A, B, D

• A(g;L)
• B(g+dg;L)
• D(g;l+dL)

représentés par a, b et d sur la carte

Calculons E_M

\(E_M = \frac{ad}{AD}\)

(0) \(\Rightarrow Pa = r = 2R_0tan(\frac{C}{2})\)

\(ad = -dr =- \frac{1}{2} \times 2R_0 \times \frac{dC}{cos^2\frac{C}{2}}\)

(1) \(ad= R_0 \times \frac{dC}{cos^2\frac{C}{2}}\)

\(AD = -R\times dL\) et \(C = 90 - L \Rightarrow AD = R \times dC\)

(2) \(AD = R \space dC\)

\(E_M =\frac{(1)}{(2)} \Rightarrow E_M = \frac{R_0}{R} \times \frac{1}{cos^2\frac{C}{2}}\)

Calculons EP

\(E_P=\frac{ab}{AB} = \frac{r \times dg}{R \times dg \times cosL}\)

(0) \(\Rightarrow E_P=\frac{2 \space R_0 \space tan \frac{C}{2} \times dg}{R \space dg \space sinC}\)

(3) \(tan\frac{C}{2}= \frac{sin \frac{C}{2}}{cos \frac{C}{2}}\) (voir le précis de trigonométrie)

(4) \(sinC = 2 sin \frac{C}{2} \space cos \frac{C}{2}\) (voir le précis de trigonométrie)

(3) et (4) \(\Rightarrow\) (5) \( \frac{tan \frac{C}{2}}{sinC}= \frac{1}{2 \space cos^2\frac{C}{2}}\) 

(5) \(\Rightarrow E_P = \frac{R_0}{R} \times \frac{1}{cos^2\frac{C}{2}}\)

\(\boxed{E_M = E_p \Rightarrow  La \space carte \space  est  \space conforme }\)

Angle entre Orthodromie et Loxodromie

Le canevas est conforme, donc la loxodromie coupe les méridiens sous un angle constant et l'angle entre les 2 routes est égale à \[\boxed{γ = \frac{dg}{2} \times sinL_m}\]

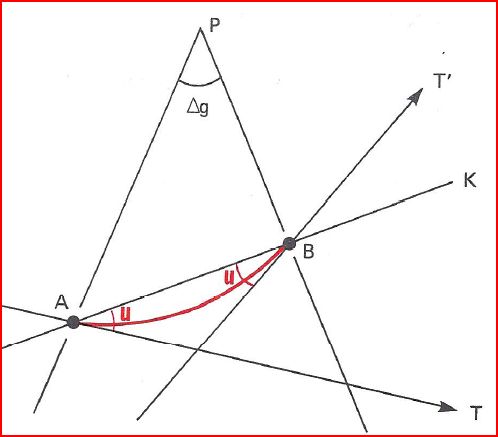
Angle u entre ortho et droite carte (pseudo correction de Givry)

(1) u = PAT - PAK

(2) u = PBK - PBT'

(1) +(2) \(\Rightarrow\) (3) 2u = PAT - PAK + PBK - PBT' = (PAT - PBT') + (PBK - PAK)

PBT' - PAT = variation d'angle de route ortho entre A et B = ΔR = Δg sinL_m

(4) PAT - PBT' = - Δg sinL_m

(5)PBK - PAK = Δg

(3) =  (4) + (5) \(\Rightarrow\) 2u = Δg - Δg sinL_m

\[\boxed{u = \frac{Δg}{2}(1-sinL_m)}\]

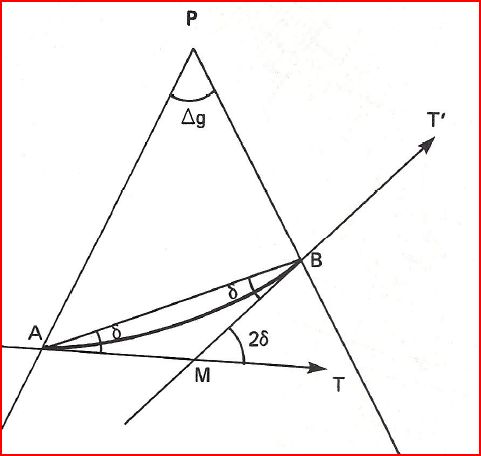
Angle δ entre loxodromie et droite carte

T'MT = 2δ = Δg

\[\boxed {δ = \frac{Δg}{2}}\]