L'orthodromie

Nous allons découvrir maintenant ce qu'est une orthodromie.

• Définitions
• Quelques remarques sur l'orthodromie
• Quelques définitions et propriétés (Vertex, Noeuds, Pôles)
• La convergence Terrestre
• La correction de Givry
• La flèche ou écart maximum entre 2 routes
• Un exercice d'application simple
• Image et positions de l'orthodromie sur un canevas mercator et la règle POLE
• L'orthodromie et la trigonométrie sphérique

 

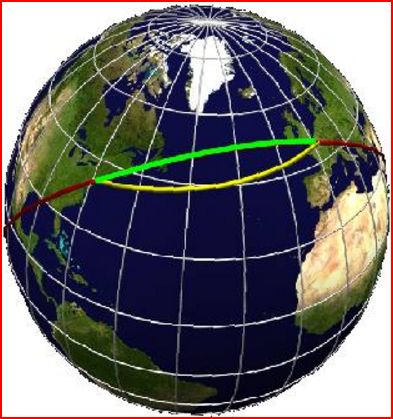
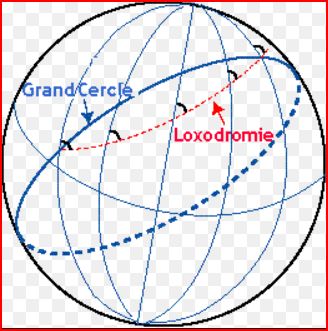
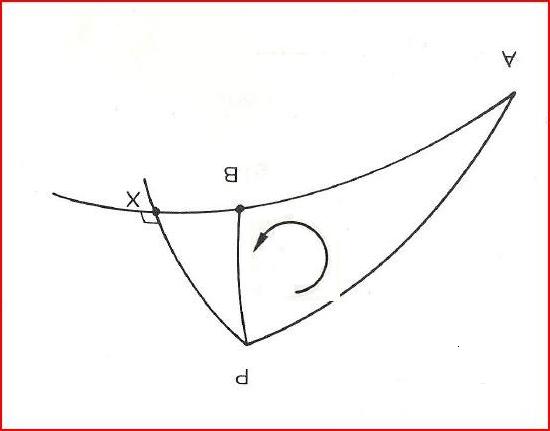
L'orthodromie désigne le chemin le plus court entre deux points d'une sphère. C'est le plus petit des deux arcs de grand cercle qui passe par ces deux points A et B sur la Terre.

Pour rappel: un grand cecle est l'intersection de la Terre avec un plan passant par le centre de la Terre.

• En rouge: le grand cercle portant l'orthodromie
• En vert: l'orthodromie (son angle de route n'est pas constant).
• En jaune: la loxodromie (Rv = cte)

Pour le navigateur, une route orthodromique désigne la route la plus courte à la surface du globe terrestre entre deux points. Dans la vie courante, cette plus courte distance entre deux points sur Terre est désignée sous le nom de «distance à vol d'oiseau» entre ces deux points. C'est aussi le trajet suivi par les ondes radios et par la lumière.

Lorsque les deux points du globe terrestre sont situés sur un même parallèle (c'est-à-dire situés à la même latitude) l'orthodromie n'est pas portée par ce parallèle (le parallèle porterait la loxodromie avec RV = 90° ou 270°), sauf si ce parallèle est lui-même un grand cercle, c'est-à-dire dans le seul cas de l'équateur.

En navigation, il sera difficile de suivre une route orthodromique. On pourra s'attacher à décomposer cette route orthodromique en une succession de routes loxodromiques. Plus cette orthodromie sera décomposée en segments loxodromiques, plus la route suivie sera proche de l'orthodromie.

En raison des vents dominants, des courants et des performances des bateaux, si la route orthodromique est la moins longue en distance, ce n'est pas forcément la plus courte en temps (la plus rapide). Par exemple la route France Caraïbe la plus rapide n'est pas la plus courte puisqu'elle suit les alizées au lieu de suivre l'orthodromie qui est bien plus au Nord. 

 

Remarques préliminaires

• Lorsque les deux points du globe terrestre sont situés sur un même méridien (c'est-à-dire situés à la même longitude), l'orthodromie est portée par ce méridien car tous les méridiens sont des grands cercles. Dans ce cas l'orthodromie est confondue avec la loxodromie (Rv= constante = 360° ou 180°)
• Entre 2 points, il n'existe qu'une seule orthodromie. La distance la plus courte entre les 2 points A et B est appelée distance orthodromique.
• La vue, les ondes magnétiques, la lumière d'un phare... suivent des routes orthodromiques.

 

 

 

Sur une carte en projection de Mercator, l'orthodromie n'est généralement pas représentée par une ligne droite mais par une ligne courbe. En effet, une carte en projection de Mercator conserve les angles. C'est la loxodromie qui coupe tous les méridiens sous un angle constant. Et qui y sera représentée par une ligne droite, car le canevas Mercator est loxodromique.

Il existe des canevas  orthodromiques sur lesquels l'orthodromie sera représentée par une droite. En conséquence, la loxodromie, elle, sera représentée sur un tel canevas par une courbe.

 

Quelques définitions et propriétés

Les Vertex X et X' de l'orthodromie

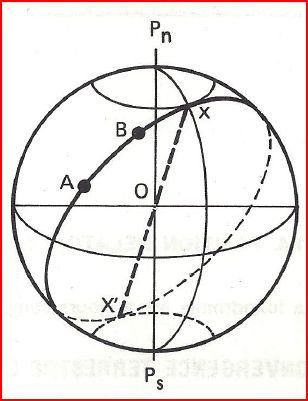
 Ce sont les 2 points les plus élevés en latitude du grand cercle qui contient l'orthodromie:

• Au Vertex l'orthodromie est tangente au parallèle et l'angle de route RV = 090° ou 270°
• Au vertex, la route orthodromique est perpendiculaire au méridien
• Si latitude de X est 50°N, alors la latitude de X' sera 50°S
• X et X' sont séparés par un écart de longitude de 180°
• les 2 Vertex sont diamétralement opposés
• L'orthodromie est la route la plus courte, donc < à 180°. Elle ne peut contenir que 0 ou 1 Vertex.

 

 

 

Les Noeuds N et N' de l'orthodromie 

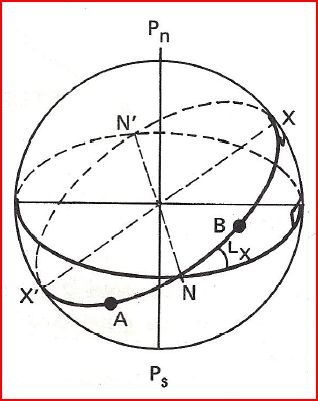
Ce sont les 2 points d'intersection du grand cercle qui contient l'orthodromie avec l'équateur:

• N et N' sont séparés par un écart de longitude de 180°
• N et X sont séparés de 90° de longitude
• En N ou N', Rv = 90 - L_X 
• L'orthodromie coupe l'équateur sous un angle égal à la latitude du Vertex X
• les 2 Noeuds sont diamétralement opposés

 

 

 

 

 

Les pôles π et π' de l'orthodromie

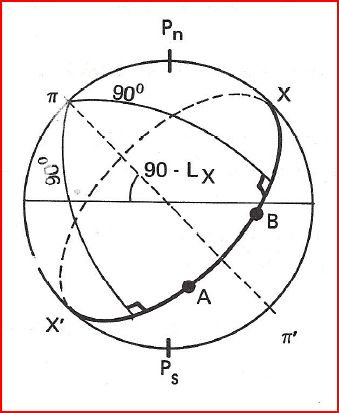
Ce sont les 2 points symétriques par rapport au centre de la Terre et situés à 90° de tous les points du grand cercle portant l'orthodromie

• La latitude du pôle d'une orthodromie est égal à la colatitude du Vertex. L_π = 90-L_X
• π et π' sont séparés par un écart de longitude de 180°
• Si latitude de π est 50°N, alors la latitude de π' sera 50°S
• les 2 pôles sont diamétralement opposés

 

 

 

 

La convergence Terrestre

La convergence Terrestre ou convergence des méridiens ΔR entre 2 points A et B est la variation d'angle de route vraie Rv orthodromique entre ces 2 points.

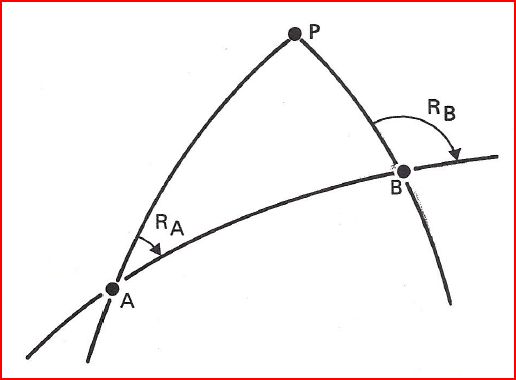
\[\boxed{ΔR = Rv_B-Rv_A}\]

On démontre en trigonométrie sphérique que:

\( tan\frac{R_B - R_A}{2} = tan\frac{dg}{2} \times \frac{sinL_m}{cos\frac{dL}{2}}\) avec \(dL = L_B-L_A\)

si les points A et B ne sont pas trop éloignés (dg<50° dL < 15° et dans les latitudes moyennes), alors:

• \(L_B - L_A\) est petit, et \(\frac{L_B - L_A}{2}\) est encore plus petit, et alors \(cos\frac{dL}{2} \# 1\) 
• \(g_B-g_A\) est petit, et \(\frac{g_B - g_A}{2}\) est encore plus petit, et alors \(tan\frac{dg}{2} \# {\frac{dg}{2}}^{rd}\)  
• \(tan\frac{R_B - R_A}{2} \# {\frac{R_B - R_A}{2}}^{rd}\)

Et on arrive alors à

\({\frac{R_B - R_A}{2}}^{rd} = {\frac{dg}{2}}^{rd} \times sinL_m \Rightarrow R_B - R_A = dg \times sinL_m\)

Si les points A et B sont assez voisins (dg<50° et dL<15° au latitude moyennes), on démontre que:

\[\boxed{ΔR = Rv_B-Rv_A = Δg \times sinLm}\]

 

La correction de givry

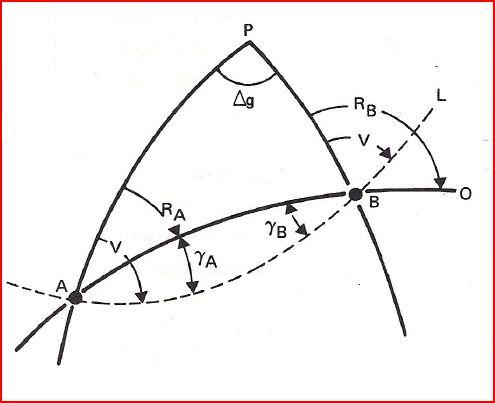
C'est l'angle γ_A ou γ_B entre la route orthodromique et la route loxodromique en A ou en B

 \[\boxed{γ =\vert{V-R}\vert}\]

 \(γ_A =V-R_A\)    (1)

 \(γ_B =R_B-V\)    (2)

Si A et B sont proches alors γ_A # γ_B # γ

(1) + (2) \(\Rightarrow 2γ=R_B-R_A=ΔR=Δg \times sinLm\)

\[\boxed{γ = \frac{Δg}{2} sinLm}\]

 

Ecart maximum entre 2 routes

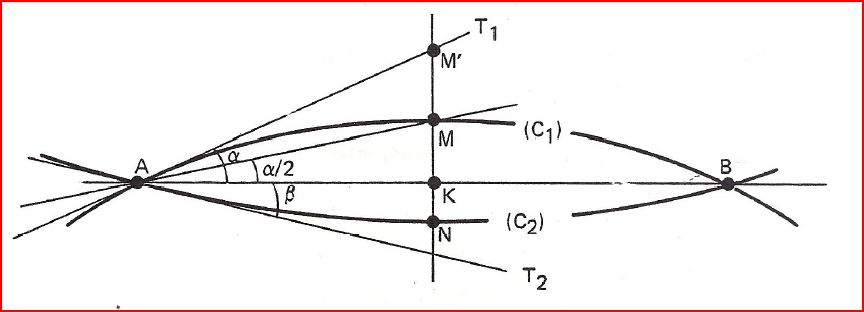
Admettons que 2 routes passent par les 2 points A et B et que leurs courbures sont régulières. La distance AB = D.

On cherche à calculer la flèche, c'est à dire la distance MN.

On a γ = α + β

\(MK = \frac{D}{2}tan\frac{α}{2}\)

Si α est petit alors \(tan\frac{α}{2}=\frac{α^{rd}}{2}=\frac{α^°}{57,5 \times 2}\)

donc \(MK = \frac{D}{2} \times \frac{α^°}{57,5 \times 2} = \frac{α^°D}{230}\)

De même, \(KN  = \frac{β^°D}{230}\)

\(MN = MK + KN =\frac{α^°D}{230}+\frac{β^°D}{230}\)

\[\boxed{f = \frac{Υ^°D}{230}}\]

 

 

Exercice d'application simple

A(00°00;145°27'E)

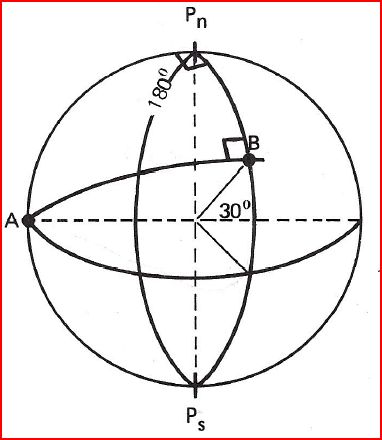
B(30°00N;124°33'W)

Calculer les angles de route en A et en B

L_A = 0, donc A est sur l'équateur et appartient au grand cercle passant par B, or  le noeud est l'intersection du grand cercle qui contient l'orthodromie avec l'équateur

A est un noeud et au noeud, Rv = 90 - L_X.

Donc Rv_A =90-30 = 060°

 

Δg= (180°-145°27')+ (180°-124°33') = 90°

N et X sont séparés de 90° de longitude

Δg = 90, donc B est un des Vertex de ce même grand cercle.

Au Vertex l'orthodromie est tangente au parallèle et l'angle de route RV = 090° ou 270°

Donc Rv_B = 090°

 

 

Calculer la distance orthodromique

AB = 90° le long d'un grand cercle \(\Rightarrow\) m = 90 x 60' = 5400 MN

 

 

Calculer la convergence terrestre

ΔR = Rv_B-Rv_A = 90-60 = 30°

 

 

Calculer la convergence terrestre avec la formule approchée

\(ΔR = Δg \times sinLm = 90 \times sin15 = 23°3\)

Les points sont espacés de 5400 MN, soit 1/4 de tour de la Terre. C'est la raison pour laquelle la formule approchée donne un résultat si différent.

Pour rappel, la formule approchée est valable pour dg<50 et dL<15 et dans les latitudes moyennes.

 

 

Quelles sont les valeurs exactes de la correction de Givry en A et B

La correction de Givry est l'angle entre les routes ortho et loxodromique.

Pour connaître cette valeur, il faut donc trouver la route loxodromique.

\(tanV = \frac{Δg}{ΔLc} = \frac{90 \times 60}{Lc_B}= \frac{5400}{1888.4}\)

\(\Rightarrow V = 70°5\)

γ_A = 70°5 - 60 = 10°5

γ_B = 90- 70°5 = 19,5°

 

Image de l'orthodromie sur un canevas Mercator Direct

De façon générale, sur tous les types de carte, et en particulier sur un canevas Mercator Direct:

• l'orthodromie tourne sa concavité vers le lieu d'Echelle minimum, qui est l'endroit ou la surface de projection est tangente à la Terre. Donc sur une carte Mercator Direct, l'orthodromie tournera sa concavité vers l'équateur.

 

 

 

L'orthodromie et la trigonométrie sphérique

La trigonométrie sphèrique permet de calculer les éléments d'une orthodromie. Vous trouverez les formules de trigonométrie sphérique dans le chapitre "Trigonométrie sphérique"

Il ne s'agit pas ici de démontrer des formules de trigonométrie sphèrique, mais de les utiliser afin de connaitre:

• RA,
• RB,
• M la distance orthodromique,
• la position des points A ou B,

lorsque les positions de A et B ne sont plus suffisamment proches, c'est à dire lorsque:

• leur écart en longitude >50°
• leur écart en Latitude >15°

On pourra aussi déterminer:

• X et X' les Vertex
• π et π' les pôles
• N et N' les noeuds

 

 

Exemple d'application : A (N38°27';W025°28) et B (N47°43';E37°25'). Calculer la distance M entre A et B .

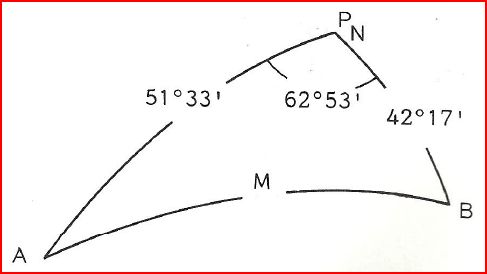
Pour tous les problèmes de triangle sphèrique, je vous conseille de faire un petit schéma et de placer sur ce shéma les éléments déjà connus.

• b = 90° - 38°27' = 51°33'
• c = 90° - 47°43' = 42°17'
• Â = 25°28' + 37°25' = 62°53'

utilisation de la Formule fondamentale:

\( cosM = cos51°33' \space cos42°17' +sin51°33' \space sin42°17' \space cos62°53'\)

\(cosM = 0.70021 \Rightarrow M=45.556° = 45°33,4' = 45 \times 60' + 33,4 = 2733,4 MN\)

 

Exemple: calculer la Rv_A (Analogie des sinus)

\(\frac{sinα}{sin42°17'}=\frac{sin62°53'}{sin45°33,4'}\)

\(\Rightarrow sinα = \frac{sin62°53' \times sin 42°17'}{sin45°33,4'} \Rightarrow α= Rv_A=57°\)

 

Calculons Rv_A et la Rv_B avec la Formule des Cotangentes

\(cotan 42°17' \space sin51°33' = cotan\hat{A} \space sin62°53' + cos51°33' \space cos 62°53'\)

\(\Rightarrow cotan\hat{A} = \frac{cotan 42°17' \space sin51°33' - cos51°33' \space cos 62°53'}{sin62°53'}\)

\(\Rightarrow tan\hat{A} = \frac{sin62°53'}{cotan 42°17' \space sin51°33' - cos51°33' \space cos 62°53'} = 1.541\)

\(\Rightarrow \boxed{\hat{A} = 57°}\)

De même, on peut écrire:

\(cotan 51°33' \space sin42°17' = cotan\hat{B} \space sin62°53' + cos51°33' \space cos 62°53'\)

\(\Rightarrow tan\hat{B} = \frac{sin62°53'}{cotan 51°33' \space sin42°17' - cos51°33' \space cos 62°53'} = 3.545\)

\(\Rightarrow \boxed {\hat{B} = 74°}\)

 

 

Trouver le Vertex Nord de l'orthodromie AB avec A (N38°27';W025°28) et B (N47°43';E37°25') et Rv_A = 057° (utilisation du pentagone)

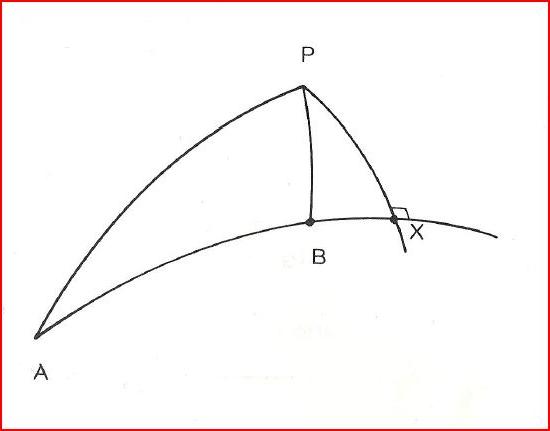
Au Vertex X, la Rv_X est perpendiculaire au méridien. Dans notre cas, Rv_X = 090°, ce qui nous donne le triangle ci-contre.

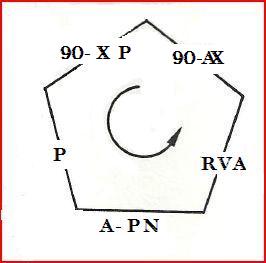
On peut dessiner le pentagone ci-contre avec l'hypoténuse = P_NA:

On peut alors écrire:

\( cos (AP_N) = cotan(P) \space cotan(Rv_A) \Rightarrow tanP = \frac{cotan(Rv_A)}{cosAP_N}\)

 

\(\Rightarrow tanP = \frac{1}{cosAP_N \times tan(Rv_A)} \Rightarrow tan(P) = \frac{1}{cos51°33' \times tan57°}  = 1.044\)

\(\Rightarrow P = 43.75° = 43°45' \Rightarrow g_x = g_A + 43°45'\)

\( g_x= W025°28' + 43°45' \Rightarrow \boxed {g_x = 018°17'E}\)

On remarque que 90-XP = L_X, et on peut écrire:

\( cos (L_X) = sin(AP_N) \space sin(Rv_A) = sin(51°33') \space sin(57) = 0.657\)

\(\Rightarrow \boxed {L_X = 48°56'"N}\)

 

 

 

Si plusieurs calculs sont à faire sur une orthodromie, on aura intérêt à calculer les coordonnées d'un Vertex afin de pouvoir utiliser la formule du pentagone. Cela aura le mérite de simplifier et de rendre les calculs suivants plus rapides.