L'étude astronomique de la marée statique va nous permettre:
- de comprendre pourquoi, sur nos côtes, nous observons une marée semi-diurne (2PM et 2 BM par jour),
- voir qu'il existe des marées diurne (1 PM et 1 BM par jour),
- de comprendre pourquoi l'heure de la marée se décale de 51 minutes en moyenne tous les jours,
- de faire le rapprochement entre les phases de la Lune et le coefficient de marée (Vives-Eaux ou Mortes-Eaux),
- de comprendre que les distances entre la Terre, le Soleil et la Lune ne sont pas constantes. En conséquence, les forces génératrices de marée et le temps séparant une PM d'une BM dépendent de la date,
- de voir que le décalage quotidien de la marée varie entre 40 minutes et 1 heure 40 minutes,
- de voir l'influence des déclinaisons de la Lune et du Soleil sur la marée.
2 PM et 2 BM par jour: la marée est semi-diurne
Le long de nos côtes atlantiques, on remarque qu'il y a 2 PM et 2 BM par jour. On dit que la marée est semi-diurne. Ainsi sur l'extrait de table de marée ci-contre, on peut voir les Heures et les Hauteurs de PM et BM pour les 1, 2, 16, 17 janvier. Comment expliquer ce phénomène?
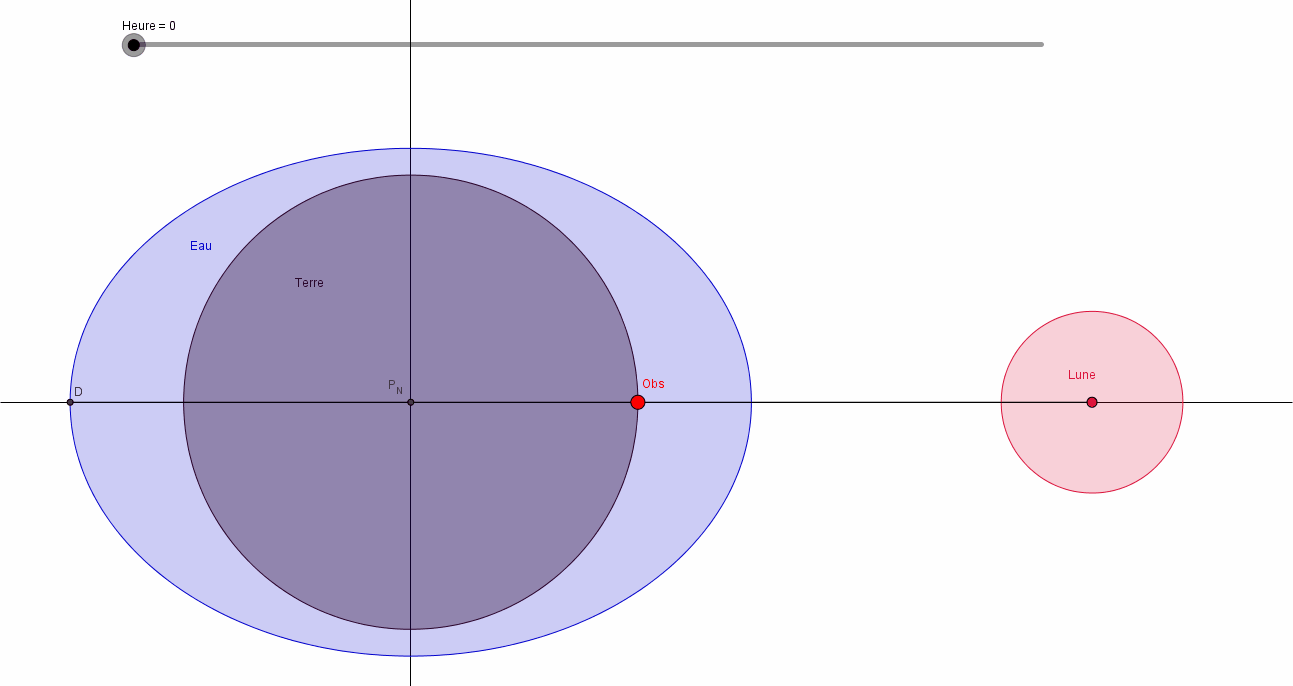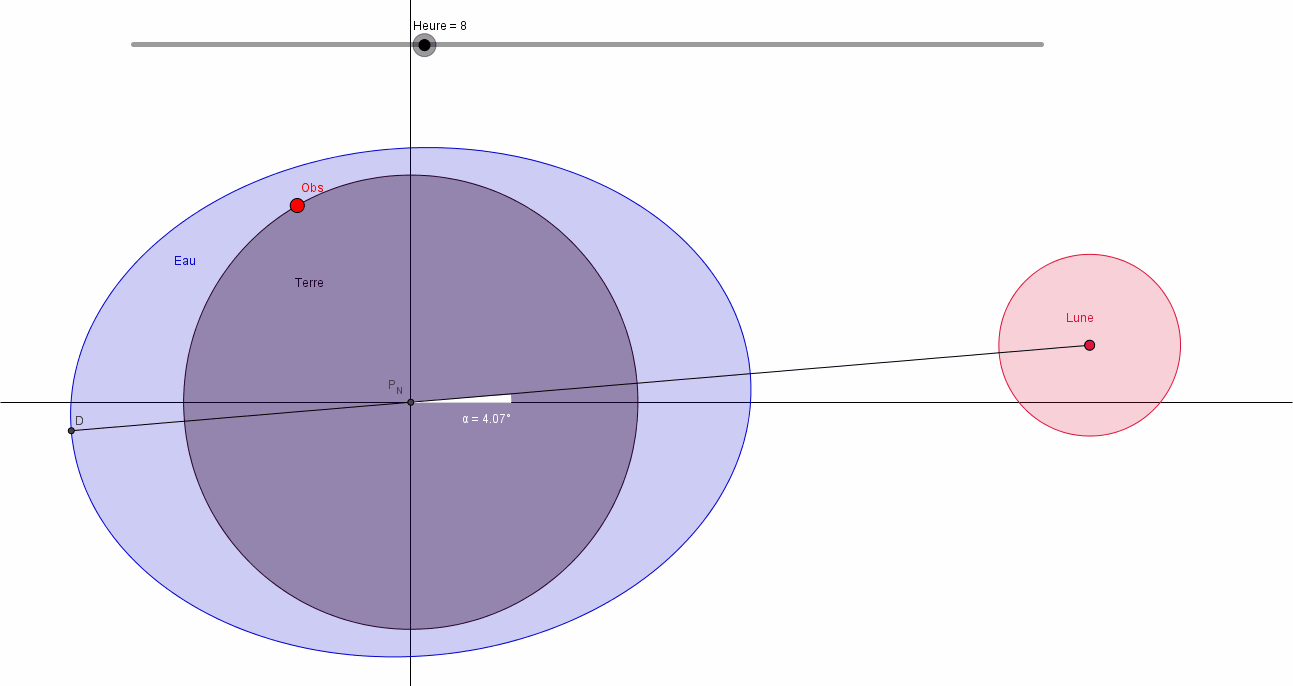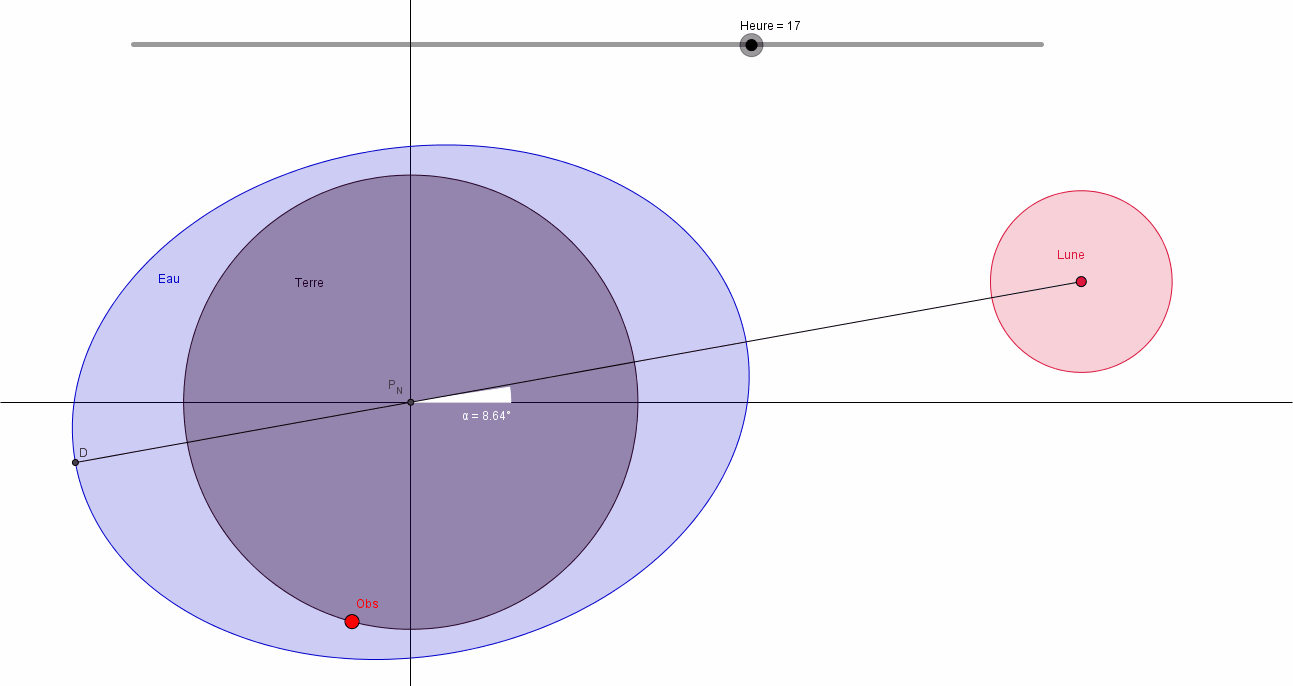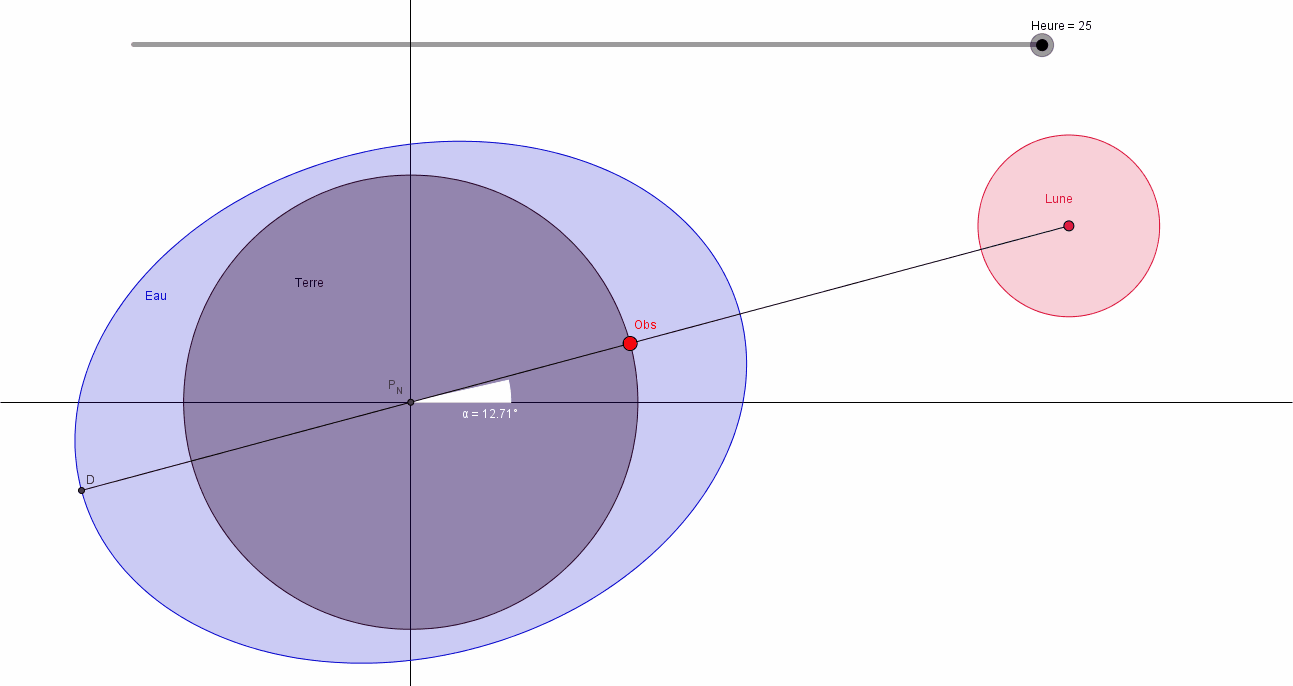
Sur une période de 24 heures, on peut considérer que les positions relatives du Soleil et de la Terre sont fixes. Considérons pour le moment qu'il en est de même pour les positions relatives de la Terre et de la Lune.
Regardons maintenant la Terre vue de dessus, c'est à dire dans l'axe Pôle Sud - Pôle Nord, et plaçons un observateur (Obs) sur la Terre. Faisons tourner la Terre sur elle-même.
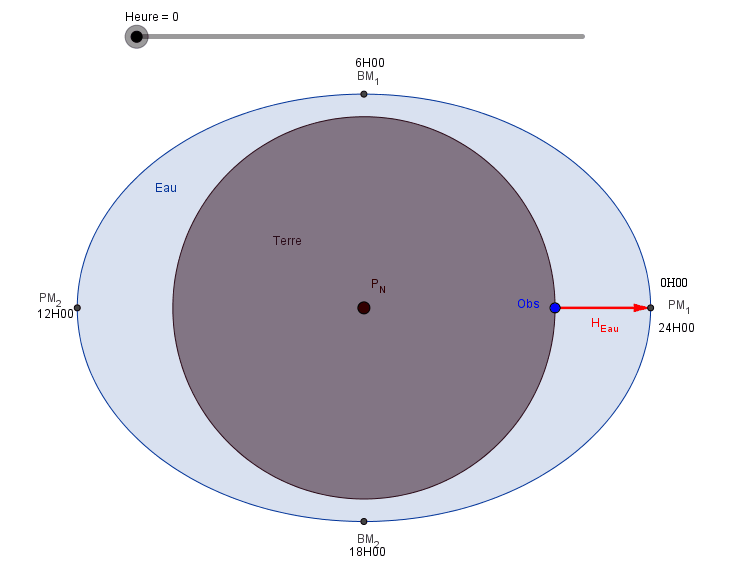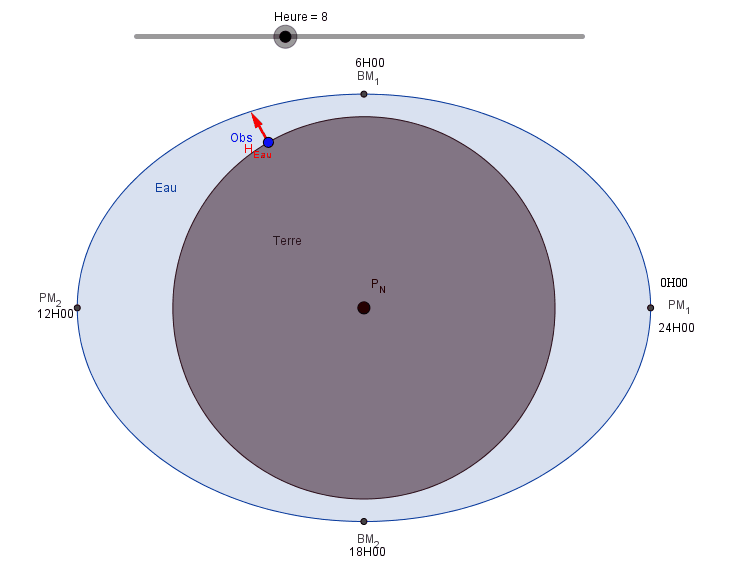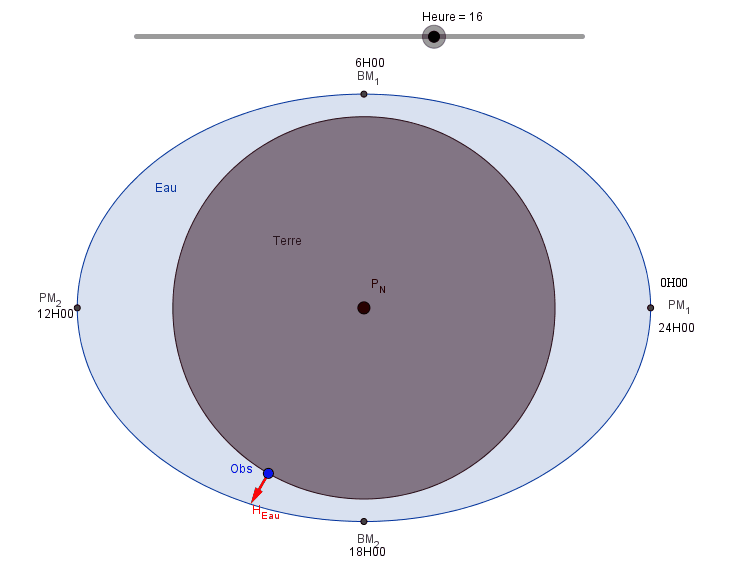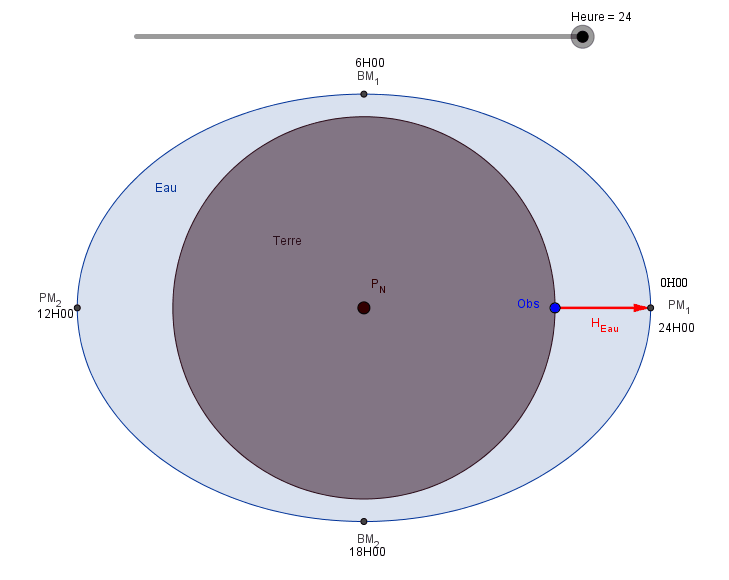
Notre observateur voit:
- à l'heure H=0: une hauteur d'eau maxi, c'est la Pleine Mer PM1,
- à l'heure H=6: soit 6 heures plus tard, une hauteur d'eau mini, c'est la Basse Mer BM1,
- à l'heure H=12: encore 6 heures plus tard, une hauteur d'eau max, c'est la Pleine Mer PM2,
- à l'heure H=18: soit toujours 6 heures après, une hauteur d'eau mini, c'est la Basse Mer BM2,
- à l'heure H=24: une nouvelle PM et ainsi de suite.
Nous pouvons dire qu'il y a une alternance PM BM avec 6 "Heures Marée" entre chaque PM et BM. La marée est semi diurne.
Pourtant il existe des endroits où la marée est diurne (1 PM et 1 BM par jour).
1PM et 1 BM par jour: la marée est diurne
A d'autres endroits, on observe des marées diurnes, c'est à dire 1 seule PM par jour.
La Lune est rarement sur le plan de l'équateur. La hauteur d'eau est forte au Zénith, et elle est faible au Nadir. Un observateur constaterait successivement une forte PM, une BM, une faible PM, une BM, et ensuite une forte PM. Ainsi, la PM du milieu passe inaperçue.
Il existe des endroits où la marée est semi-diurne, d'autres où elle est diurne, et d'autres encore où elle est mixte (diurne, ou semi-diurne, en fonction des déclinaisons de la Lune et du Soleil).
Le décalage quotidien de la marée
Tous les jours, on s'aperçoit que l'heure de la marée avance. Ainsi dans le tableau ci-dessus, on remarque que la 2ème PM du 10 est à 15h35 et celle du 11 est à 16h25 soit 50 minutes plus tard.
Dans le paragraphe précédent, nous avons considéré que les positions relatives de la Terre et de la Lune étaient fixes, Nous avons en conséquence trouvé que l'écart entre PM et BM consécutives était de 6 heures exactement. Ce qui n'est pas exact.
Décrivons ce qui se passe réellement sur environ 24 heures. La Lune est un satellite de la Terre, et sa révolution (période synodique) est de 29.5 jours (1 mois lunaire):
- Pendant que la Terre fait 1 tour sur elle-même, la Lune tourne de 1/29.5 tour autour de la Terre, soit 360/29.5 = 12.2 °
- La Terre tourne sur elle-même à la vitesse de 360° en 24 heures, soit 15°/heure.
Pour que notre observateur soit à nouveau sur le méridien de la Lune, et constate à nouveau la PM, il faudra que la Terre tourne encore de 12.2° à la vitesse de 15°/h, soit \(\frac{12.2}{15}\)=0.81 heure de plus, soit 48 minutes. Pendant ces 48 minutes, la Lune avancera de environ \(\frac{12.2}{24}\)=0.5°, et la Terre devra tourner d'autant: \(\frac{0.5}{15}\) =0.03heures, soit encore 2 min. Ce qui nous amènera à un décalage de 50 minutes par jour.
Nous verrons un peu plus loin que ce temps est une valeur moyenne, et que ce décalage varie dans le temps.
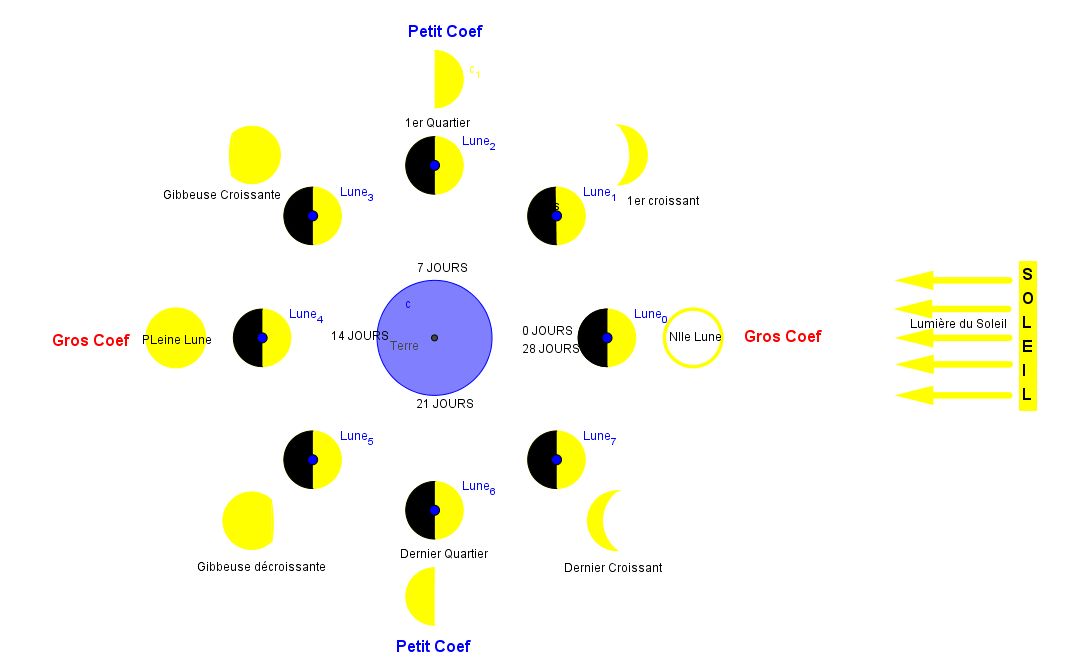
La marée et les phases de la Lune
Agrandissons notre échelle pour arriver au temps du mois Lunaire, et voir les positions relatives du système Terre-Soleil-Lune.
- A cette échelle, la position de la Terre par rapport au Soleil peut être considérée comme fixe
- La Lune fait un tour complet autour de la Terre lors de sa révolution synodique. Elle est donc vue différemment depuis la Terre en fonction de son âge.
- la Nouvelle Lune: la Lune est dans l'axe Terre-Soleil. Elle est invisible (on "voit" la face qui est dans l'ombre) . Le coefficient de marée est fort. C'est la Syzygie.
- le 1er croissant: la Lune commence à apparaitre en se décalant de l'axe Terre-Soleil. Le coefficient de marée diminue.
- 1er Quartier: la Lune est en quadrature avec l'axe Terre-Soleil. La moitié de la Lune est visible depuis la Terre. Le coefficient de marée est faible. C'est la quadrature.
- gibbeuse croissante: le coefficient de marée augmente.
- Pleine Lune: le coefficient de marée est fort (syzygie).
- gibbeuse décroissante: le coefficient de marée diminue.
- Dernier Quartier: le coefficient de marée est faible (quadrature).
- dernier croissant: le coefficient de marée augmente.
Pour savoir si la lune est décroissante, il suffit d'imaginer une barre du côté de la Lune ou il manque une partie visible. Si on peut imaginer un d, alors La Lune est décroissante. (c et l donne d donc décroissante).
La Lune croissante: si la Lune n'est pas décroissante, alors elle est croissante. Ou encore en imaginant toujours cette barre verticale, on pourrait lire un P comme Premier Croissant.
En observant les phases de la Lune, on peut déterminer si le coefficient de marée est fort, faible, en augmentation ou en diminution.
Notons que la Lune, de par sa révolution propre, nous montre toujours la même face.
La 1ère Loi de KEPLER: les distances Lune/Terre/Soleil ne sont pas constantes
En astronomie, des lois décrivent les propriétés principales du mouvement des planètes autour du Soleil (dans un système héliocentrique). Elles ont été découvertes par Johannes Kepler (1571-1630).
Enoncé de la 1ère loi de Kepler dite "Loi des Orbites": Les planètes du système solaire décrivent des trajectoires elliptiques, dont le Soleil occupe l'un des foyers.
La Lune est un satellite de la Terre et décrit dans un système géocentrique une trajectoire elliptique, dont la Terre est l'un des foyers (si on considère que le centre d'inertie du système Terre-Lune est confondu avec le centre de la Terre).
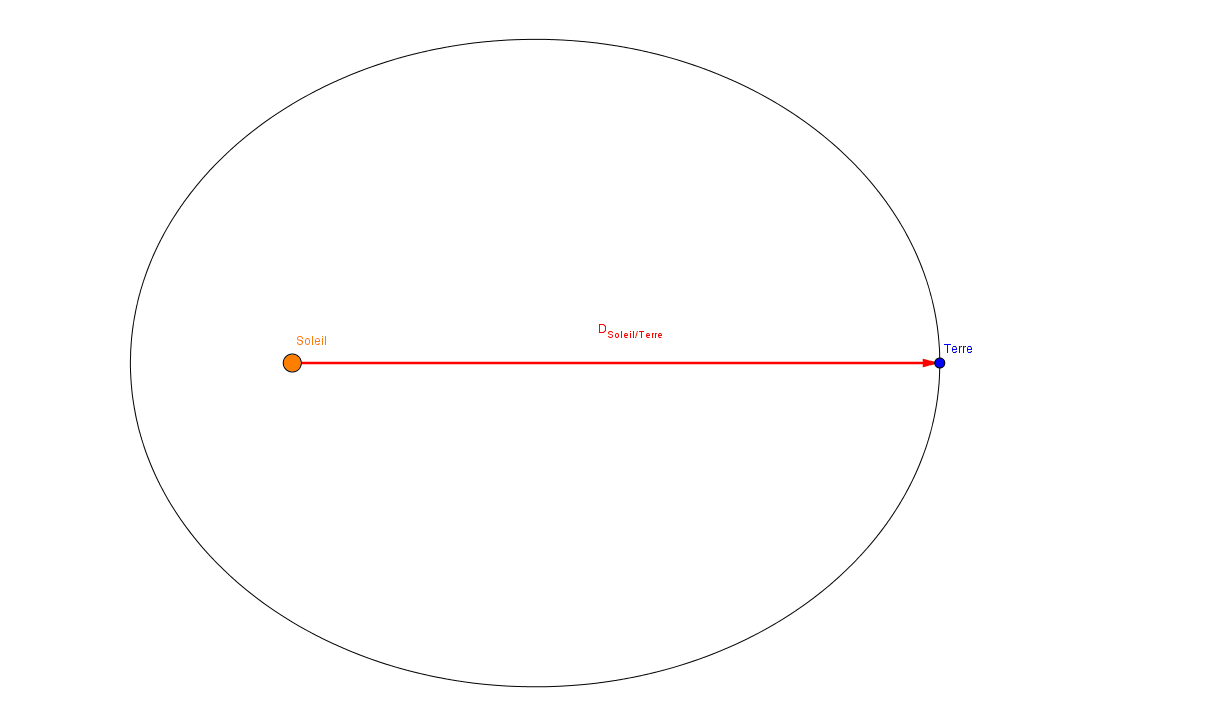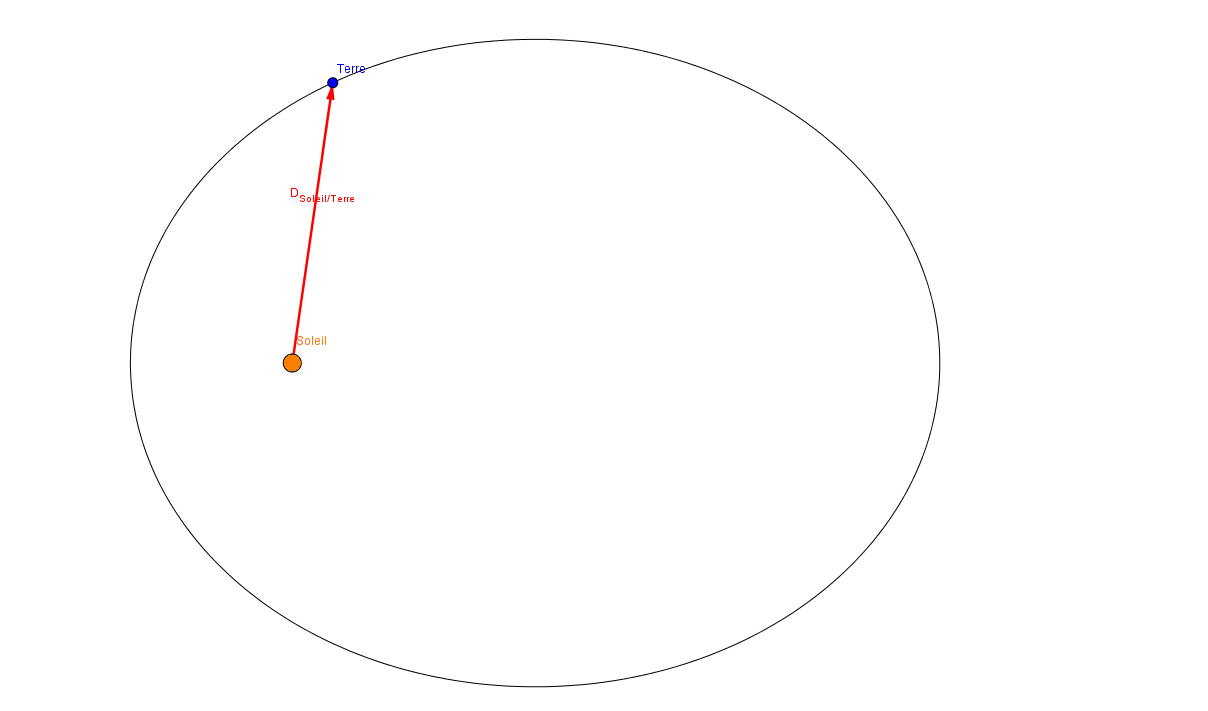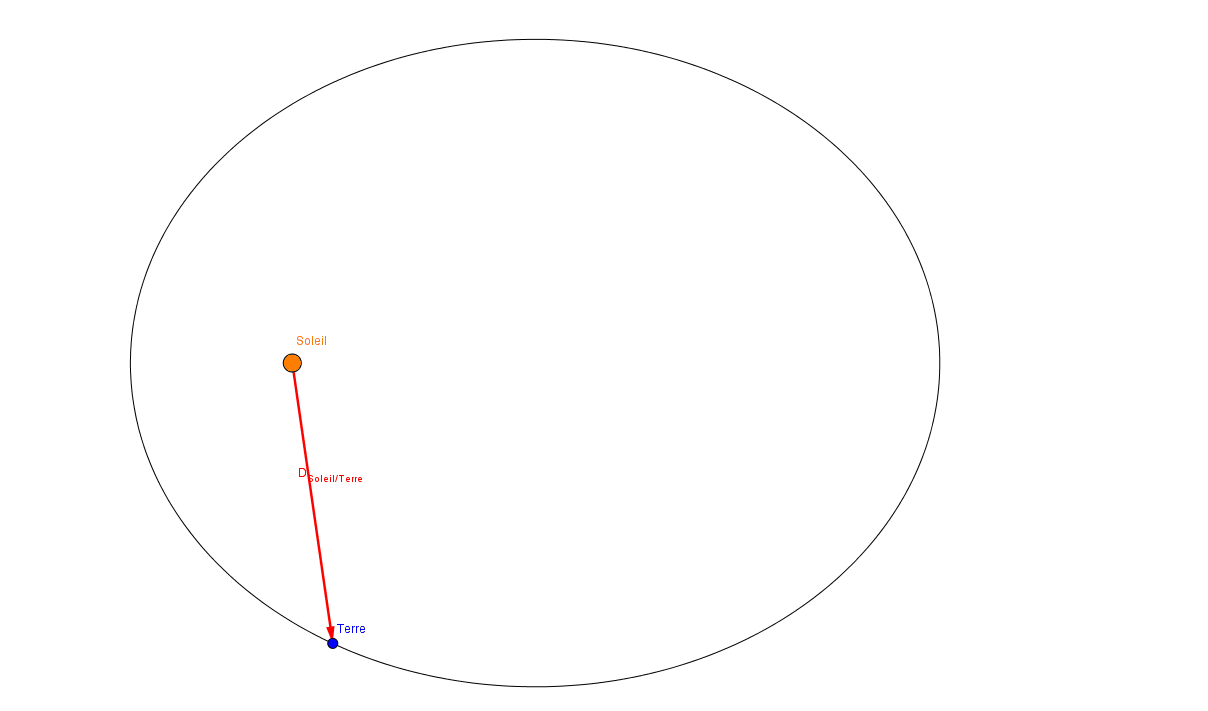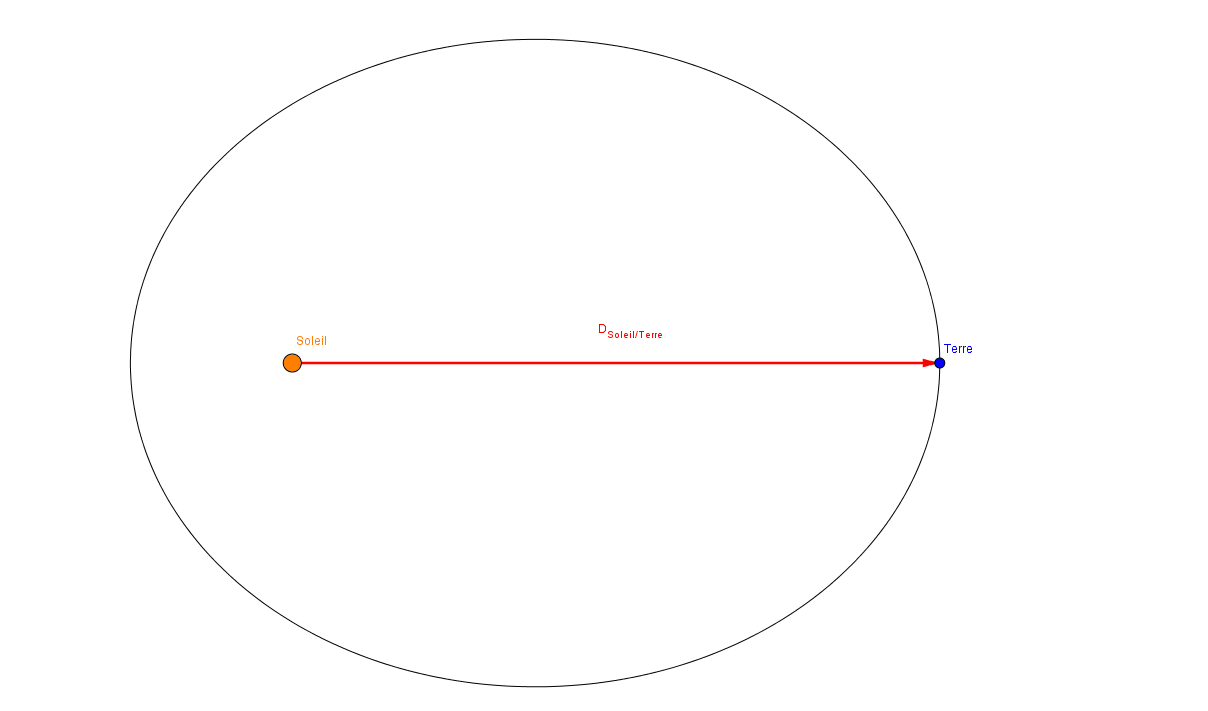
Les distances Terre-Lune et Terre-Soleil ne sont pas constantes. En conséquence, et d'après la théorie de Newton, les forces génératrices de la marée varient en fonction des positions relatives de la Lune, du Soleil et de la Terre, donc du temps.
La 2ème Loi de KEPLER: le décalage de la marée varie entre 40min et 1h40min par jour
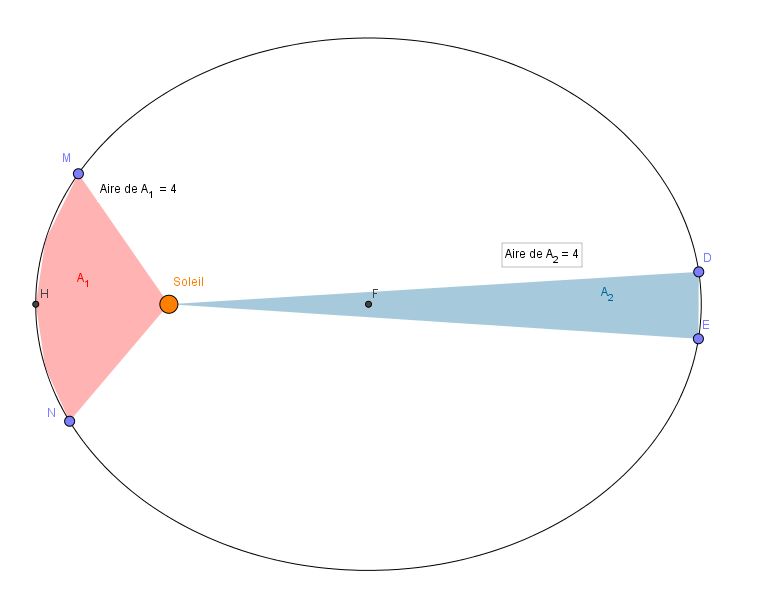
Enoncé de la 2ème loi de Kepler dite "Loi des aires":
Considérons la Terre tournant sur son orbite autour du Soleil. Au moment T1 cette planète se situe en E. A l'instant T2, elle se trouve en D. Alors pendant le temps T=T2-T1, le segment Soleil-Terre balaye l'aire A2 (en bleu)
6 mois plus tard, la Terre se retrouve au point M. Pendant le même temps T, elle se déplace pour se retrouver en N. Alors le segment Soleil-Terre balaye l'aire A1 (en rouge).
La 2ème loi de Kepler précise que l'aire A1= l'aire A2
En conséquence, plus la Terre est proche du Soleil, plus elle se déplace rapidement. Il en va de même pour la Lune sur son orbite autour de la Terre. Pendant le même temps T, la Lune peut se déplacer:
- de plus de 12.2°/24 heures. Le décalage de la Lune peut atteindre 25° (soit 25/15=1.66 heure=1h40min) lorsqu'elle est proche de la Terre.
- de moins de 12.2°/24/heures. Le décalage de la Lune peut se limiter à 10° (soit 10/15=0.66=heure=40min) lorsqu'elle est loin de la Terre.
Le 16 janvier la 1ère PM a lieue à 07h04, et le 17 janvier à 07h41 soit 36 minutes d'écart.
Le 18, la dernière PM à lieu à 22h24, celle qui se situe environ 24 heures après a lieue le 20 à 00h08, soit un décalage de1h44. Le cycle étant d'une durée supérieure à 24 heures, certains jours ne verrons qu'une seule PM ou BM. C'est le cas du 19 qui ne voit qu'une seule PM à 11h00.
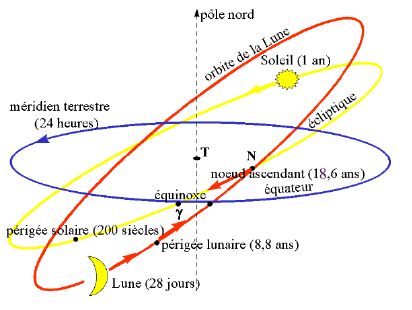
Positions de la Lune et du Soleil par rapport à la Terre
- en bleu: l'equateur terrestre, la Terre tourne sur elle même en 24 heures
- en jaune: l'écliptique (position du Soleil sur la Terre) inclinée à 23°27' par rapport à l'equateur. La position du Soleil parcourt l'ellipse jaune en 1 an
- en rouge: la trace de l'orbite Lunaire sur la Terre, inclinée de 5°08' par rapport au Soleil. La position de la Lune parcourt l'ellipse rouge en 28 jours
Quelques points caractéristiques:
- Equinoxes de Printemps et d'Automne: la déclinaison du Soleil est nulle, le Soleil est sur l'équateur. Le temps de jour est égal au temps de nuit. Le Soleil se lève au relèvement 090 et se couche au 270.
- Les solstices d'Eté: la déclinaison du Soleil est de 27°23' N, c'est l'été. Le Soleil se lève au relèvement 067 (90-23) et se couche au relèvement 297 (270+23). Le temps de jour est maximal et le temps de nuit minimal.
- Les solstices d'Hiver: la déclinaison du Soleil est de 27°23' S, c'est l'hiver. Le Soleil se lève au relèvement 113 (90+23) et se couche au relèvement 247 (270-23). Le temps de jour est minimal et le temps de nuit est maximal.
- "Les marées du siècle" (coefficient de 119 et 120) se produisent tous les 18.6 ans
Pour plus de renseignements, je vous invite à lire ou a regarder:
- Un article de Voiles et voiliers: les phénomène des grandes marées
- Tous sur orbite: une série de reportage sur les orbites. Le lien vous mène vers un condensé de ces 52 épisodes. Vous pouvez si cela vous intéresse regarder tous les épisode en faisant une recherche sur Youtube: tous en orbite.
- Science et Vie
La décilnaison de la Lune fait que nous la verrons plus ou moins penchée
On comprend que la marée puisse prendre plusieurs forme en fonction des positions relatives du système Terre-Lune-Soleil et de la position géographique de l'observateur.
Conclusions
La théorie de la marée statique de Newton permet d'expliquer quelques grands principes:
- La périodicité de 12 heures lunaires qu'il conviendra de transformer en heure marée pour réaliser un graphe de marée, car l'écart entre BM et PM n'est pas égal à 6 heures solaires, mais à 6 heures Lunaires (voir la partie Pratique sur le sujet),
- La relation entre les phases de la Lune et l'amplitude de la marée,
- Les forces génératrices de la marée,
- Les variations de l'amplitude de marée. En même lieu avec la même phase de la Lune, l'amplitude de la marée n'est pas constante,
- C'est quand la Terre, la Lune et le Soleil sont dans le même plan que les coefficients de marée seront les plus forts,
- La marée la plus grande devrait se réaliser lorsque coïncident toutes les conditions:
- syzygie,
- passage de la Lune à son périgée,
- éclipse de Lune ou de Soleil,
- Equinoxe de printemps ou d'automne,
- dans ce cas, les actions conjuguées du Soleil et de la Lune sont maximales).
Les échecs de la théorie statique de Newton
Cependant, cela n'explique pas certaines observations:
- Par Calcul, on trouve une marée lunaire de 35 cm et une marée solaire de 16 cm au maximum. La somme des 2 ferait une marée de 51 cm!!
- Comment expliquer des marnages de 15 m dans la baie du Mont Saint-Michel,
- On constate un écart très important entre les PM et les syzygies (Pleine Lune et Nlle Lune) que cette théorie n'explique pas; dans le tableau des coefficients de marée ci-contre, on voit la Pleine Lune le 3 à 16h38 avec un coeff 102. Le Coeff le plus fort sera pourtant le 5 à 05h47...
- Cette théorie néglige l'effet des continents qui changent la célérité et la trajectoire de l'onde de marée,
Si la théorie de la marée statique peut expliquer une allure générale des marées, elle est très insuffisante pour des applications pratiques et la prédiction des marées.