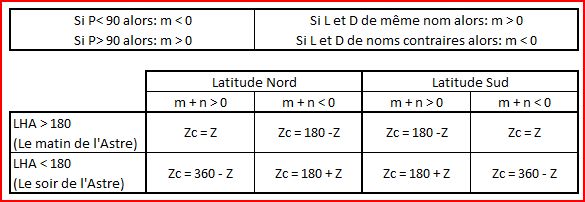
Les tables de Bataille servent à calculer Zc. Une précision au degré ou au 1/2 degré sera suffisante. La direction de l'astre sera tracée à l'aide de la règle cras qui est graduée au degré prés. Une valeur approximative de l'azimuth Zc pourrait être relevée au compas au risque de s'abimer les yeux!!
Pour simplifier les tables et ne pas multiplier le nombre de pages nécessaires, on acceptera d'arrondir les valeurs d'entrée P, D et L au degré le plus proche, ce qui nous donnera une précision suffisante.
Certaines colonnes et lignes seront masquées, la différence avec la colonne ou la ligne adjacente n'étant pas significative.
Les tableaux contiendront des nombres à 2 décimales. Cette précision sera suffisante pour trouver un resultat au degré près.
1ère Méthode
tan(90−Z)cos(90−P)=−cosPsinL+tanDcosL
- table 1 : f(x;y) = cosx siny
- table 2 : g(x;y) = tanx cosy
Table 1
Etude de m = - sinL cosP
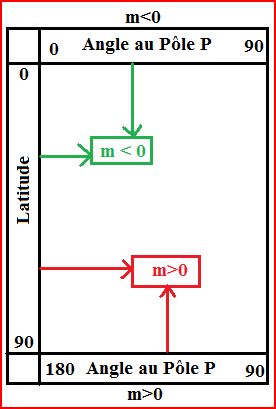 Le signe de m = -sinL cosP varie en fonction des valeurs de P. Le tableau sera fait avec des fonction sans signe + ou -. Ce sera alors au navigateur de déterminer les signes.
Le signe de m = -sinL cosP varie en fonction des valeurs de P. Le tableau sera fait avec des fonction sans signe + ou -. Ce sera alors au navigateur de déterminer les signes.
Vu depuis la sphère locale la latitude varie de 0 à 90° donc sinL > 0
- si P<90 alors cosP > 0, en conséquence, m = -sinL cosP < 0
- si P > 90 alors cosP < 0, en conséquence, m = -sinL cosP > 0
- cosP = cos(-P), donc nous aurons un tableau symétrique par rapport a P = 0
Pour trouver m, nous aurons besoin d'un tableau calculant sinL cosP, sans signe:
- la valeur de P<90 sera lue sur le dessus du tableau avec m <0
- la valeur de P > 90 sera lue sur le bas du tableau avec m > 0
- la valeur de L sera lue à gauche du tableau
- On lira le résultat m dans la "case intercection" de P et L, à l'interieur du tableau, et on lui donnera un signe
Appliquer la régle
- si P > 90 alors m > 0
- si P < 90 alors m < 0
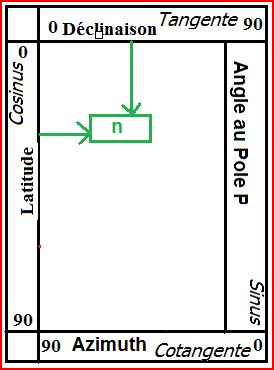 Table 2: n = tanD cosL
Table 2: n = tanD cosL
- Si D et L sont de mêmes noms, alors n > 0
- Si D et L de noms différents alors n < 0
Pour trouver n, nous aurons besoin d'un tableau calculant tanD cosL, sans signe:
- la valeur de D sera lue sur la ligne du haut.
- la valeur de L sera lue à gauche du tableau
- On lira le résultat m dans la "case intercection" de D et P, à l'interieur du tableau, et on lui donnera un signe
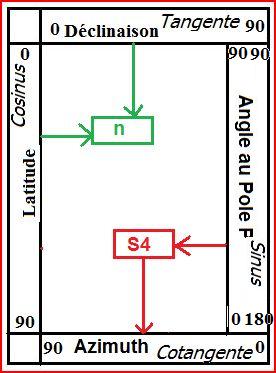 Table 2: cotanZ sinP
Table 2: cotanZ sinP
Rappelle de trigonométrie:
- tan(90 - x) = cotan(x)
- sin(90 - x) = cos x
ce qui va permettre de trouver des entrée et des sorties des 4 côtés de la table.
on calcule d'abord S4 = m + n
- chercher l'angle P dans la colonne de droite
- chercher S4 le long de la ligne
- lire l'azimuth Z sur la ligne du bas
Nous avons trouver Z!!
 2ème Méthode
2ème Méthode
cosD×sinP = m = cosHv×sinZ
- table 1 : f(x;y) = cosx siny
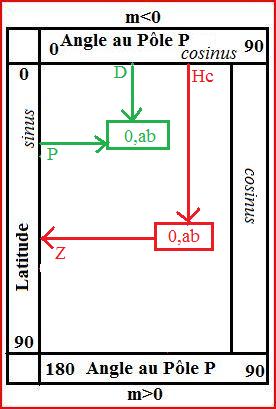
Seule la Table 1 nous sera utile pour déterminer Z, à condition de connaitre Hc.
- 1ère utilisation de la Table 1 avec D (coté cosinus) et P (coté sinus) en vert pour trouver un nombre ayant la forme 0,ab
- 2ème utilisation de la Table 1 avec Hv (coté cosinus), aller j'usqu'a trouver 0,ab pour trouver Z (côté sinus)
Nous avons trouver Z!!
Trouver Zc
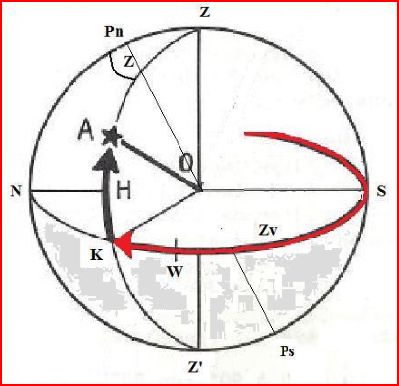
Pour trouver Zc, nous n'avons pas tenu compte des signes de L, D, P. En conséquence, Z est toujours un angle inférieur à 90° alors que 0 < Zv <360. Il convient maintenant de se placer sur la sphère locale, et de placer les différents éléments en notre possession sur cette sphère locale pour déterminer Zc en fonction de Z. La définition de la sphère locale vous a déjà été présentée dans le chapitre Les Coordonnées Horizontales
tan(90−Z) cos(90−P) = −cosP sinL + tanD cosL = m + n
cos(90 - x) = sin(x) \(\Rightarrow\) cos(90 - P) = sinP avec 0 < P < 180
\(\Rightarrow\) cos(90 -P) > 0
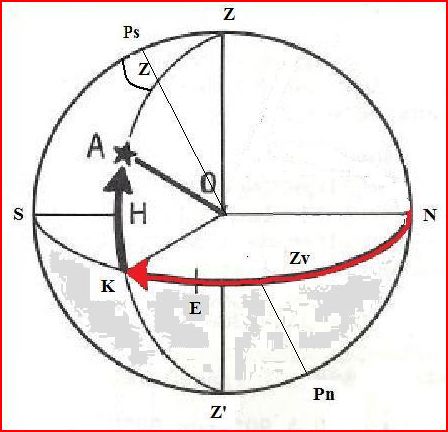
Latitude Nord
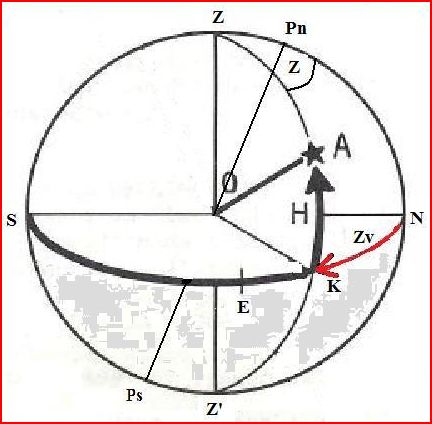
Si m + n > 0,
\(\boxed{Zv=Z}\)
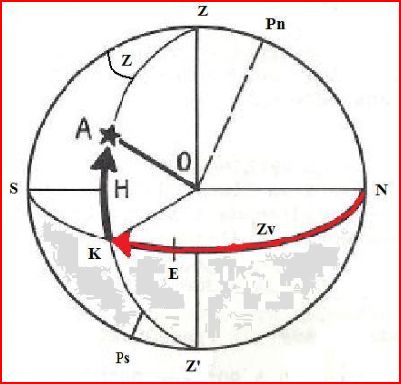
\(\boxed{Zv = 180 - Z}\)
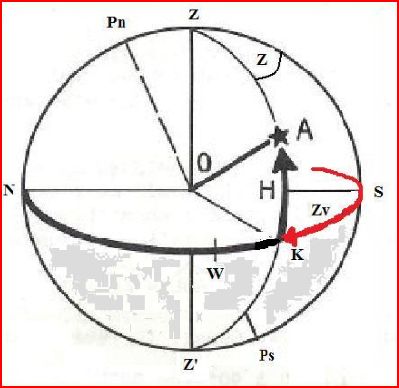
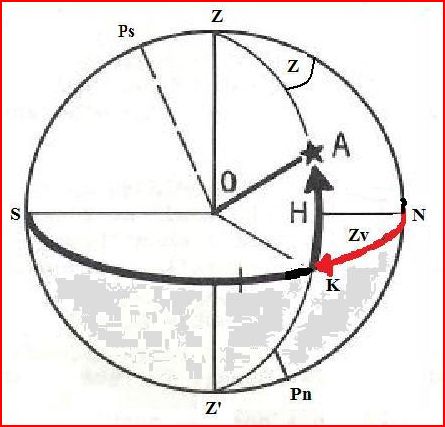
Si m + n < 0
\(\boxed{Zv = 180 + Z}\)
\(\boxed{Zv = 360 - Z }\)
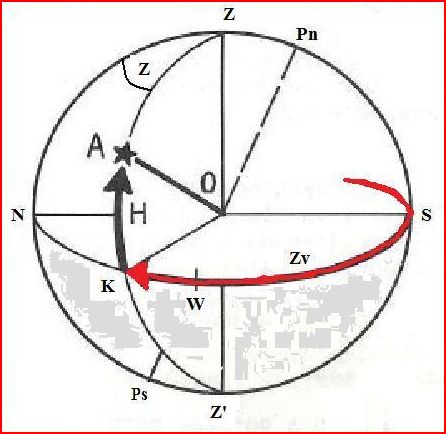
Latitude Sud
Au matin de l'astre, LHA > 180
Si m + n > 0,
\(\boxed{Zv = 180 - Z }\)
Si m + n < 0
\(\boxed{Zv = Z}\)
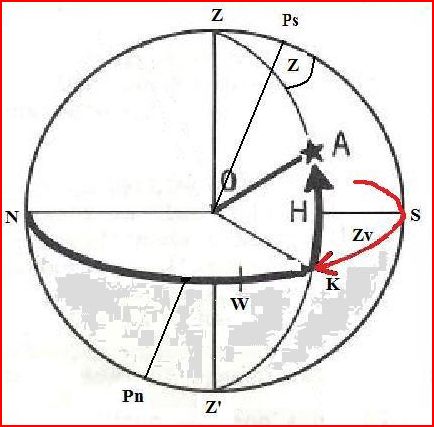
Au soir de l'Astre, LHA < 180
Si m + n < 0
\(\boxed{Zv = 360 - Z}\)
Si m + n > 0,
\(\boxed{Zv = 180 + Z }\)
Résumé
Ce résumé est à garder précieusement ou à coller dans la boite de votre sextant pour s'y référer à chaque point.