Les différences de pression créent des forces de pression qui vont créer le mouvement de l'air. Une fois posées les hypothèses géostrophiques, l'équation du mouvement devient: \[\overrightarrow{Fp_h} + \overrightarrow{Fc_h} = \overrightarrow{0}\]
Cette équation fait apparaitre l'équilibre entre les composantes horizontales des forces de pression et de Coriolis.
Etudions les composantes horizontales des forces de pression
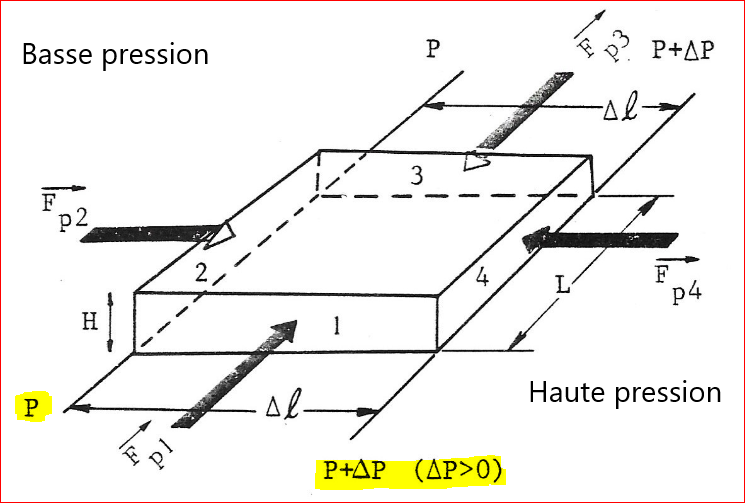
Considérons une particule d'air ayant une forme de parallélipéde rectangle en équilibre sur le lan vertical. Elle est positionnée sur une carte de ligne isobares qui est par définitiion un support horizontal.
De façon générale, \(P = \frac{force}{surface} = \frac{F}{S} \Rightarrow F = P \times S\). De plus les forces de pression sont perpendiculaires à la surface sur laquelle elles s'exercent.
Examinons ces forces:
Les forces \(\overrightarrow{Fp_1}\) et \(\overrightarrow{Fp_3}\) sont opposées et \(\vert \overrightarrow{Fp_1} \vert = \vert \overrightarrow{Fp_3} \vert \Rightarrow \overrightarrow{Fp_1} + \overrightarrow{Fp_3} = \overrightarrow{0}\). En effet les lignes isobares sont parallèles dans le cas de notre figure, et peuvent être considérées comme parallèles à petite échelle.
Sur la face 2 : \(Fp_2 = PS\)
Sur la face 4 : \(Fp_4 = (P+\Delta P)S\) avec \(\Delta P > 0\)
\(\Rightarrow\) La résultante de \(\overrightarrow{Fp_4} +\overrightarrow{Fp_2}\) est dirigée des Haute Pressions vers les Basses Pressions
\(\Rightarrow \vert \overrightarrow{Fp_4} +\overrightarrow{Fp_2} \vert = (P + \Delta P).S - P.S = \Delta P.S\)
En conséquence, la somme des forces de Pression est dirigée des Hautes Pressions vers les Basses Pressions et son module est \(\vert \overrightarrow{Fp_h} \vert = \Delta P.S \)
Dans cette expression, S est la surface surlaquelle s'appuie la force \(\overrightarrow{Fp_4}\) , soit \(S=L \times H = \frac{V}{\Delta L} = \frac{m}{\rho}. \frac{1}{\Delta L}\)
En effet : \(V = L \times H \times \Delta L \Rightarrow L \times H = \frac{V}{\Delta L} = S\) et
La masse volumique \(\rho = \frac{m}{V} \Rightarrow V = \frac{m}{\rho}\)
Il en résulte : \[\vert \overrightarrow{Fp_h} \vert = \frac{m}{\rho}. \frac{\Delta P}{\Delta L}\]
Etudions les composantes horizontales de la force de Coriolis
La force de Coriolis s'exprime: \(\overrightarrow{Fc}= -2m \overrightarrow{\Omega} \wedge \overrightarrow{V}\) et fait apparaitre que la force de Coriolis \(\overrightarrow{Fc}\) est:
perpendiculaire au vecteur vitesse
- située à droite de \(\overrightarrow{V}\) dans l'hémisphère Nord (ou encore que \(\overrightarrow{V}\) est à gauche de \(\overrightarrow{Fc}\))
- située à gauche de \(\overrightarrow{V}\) dans l'hémisphère Sud (ou encore que \(\overrightarrow{V}\) est à droite de \(\overrightarrow{Fc}\))
- \(\vert \overrightarrow{Fc_h} \vert = 2 \times m \times \vert \overrightarrow{\Omega} \vert \times \vert \overrightarrow{V} \vert \times sin\varphi\)
- Pour une même différence de pression, la force de Coriolis dépend de la latitude. Elle est nulle à l'équateur.
Conclusion
\(\overrightarrow{Fp_h} + \overrightarrow{Fc_h} = \overrightarrow{0} \Rightarrow \vert \overrightarrow{Fp_h} \vert = \vert \overrightarrow{Fc_h} \vert\)
\(\Rightarrow \frac{m}{\rho}. \frac{\Delta P}{\Delta L} = 2 \times m \times \vert \overrightarrow{\Omega} \vert \times \vert \overrightarrow{V} \vert \times sin\varphi\)
Définissons f, le facteur de Coriolis \[ \boxed{f = 2 \times \Omega \times sin\varphi}\]
alors, \(\frac{m}{\rho}. \frac{\Delta P}{\Delta L} = m \times f \times \vert \overrightarrow{V} \vert\)
\[\Rightarrow \boxed{Vg = \frac{1}{\rho f } \frac{\Delta P}{\Delta L}}\]
Avec
- \(\rho\) : masse volumique de l'air # \(1.225 Kg/M^3\)
- \(f\): facteur de Coriolis = \(2. \Omega. sin\varphi\) en rd/s
- \(\Omega\) vitesse de rotation de la Terre a 1 tour / 24 heures soit \(\frac{2 \Pi}{86164}= 7.29 . 10^-5\) rd/s
- \(\Delta P\) difference de pression entre 2 isobares en Pa
- \(\Delta L\) distance entre les 2 isobares en m
- Vg: vent géostrophique en m/s
Application
Sur une carte météo, au large de Brest, \(\varphi = 47°30"\), les isobares 1000 hpa et 10005 hpa sont espacées de 220 km. Quelle est la vitesse du vent?
\(f = 2 \times 7.29 . 10^5 \times sin47,5° = 1.075 \times 10^-4\)
\(Vg = \frac{1}{1.225 \times 1.075 \times 10^-4} \times \frac{500}{220 \times 10^3} \approx 17m/s \approx 34Kts\)