Le vent géostrophique est le résultat d'un modèle mathématique simplifié dans lequel les forces de frottement et l'accélération absolue de la particule sont nulles. \(\overrightarrow{Ff_h}=\overrightarrow{0}\) et \(\overrightarrow{\Gamma_a}= \overrightarrow{0}\)
Il s'agit maintenant de tenir compte autant que faire se peut de ces deux éléments supplémentaires
Introduction des forces de frottement: \(\overrightarrow{Ff_h}\)
Le géostrophisme considère une planète sans continents et sans étendue d'eau, faite d'une matière uniforme et n'occasionnant pas de frottement. Ce n'est cependant pas la réalité. En effet, si cette hypothèse est potentiellement vraie dans les hautes altitudes, ce n'est pas le cas dès lors que l'on s'approche de la surfac de la Terre.
En s'approchant de la surface de la Terre, nous rentrons dans la couche atmosphérique appelée "couche turbulente". Cette couche s'étend depuis la surface de la Terre jusqu'a une altitude de 1500 a 2000 m de hauteur.
La surface de la Terre constitue un obstacle à l'écoulement de l'air. Les forces de frottement résultant de la présence de cet obstavle sont maximales à son contact et s'atténuent à mesure que l'on s'élève dans la couche turbulente, pour être nulle dans l'armosphère "libre".
La prise en compte de ces forces de frottement nous amène à écrire l'équation du mouvement définie dans les chapitres précédents sous la forme: \[ \overrightarrow{Fp_h} + \overrightarrow{Fc_h} + \overrightarrow{Ff_h} = \overrightarrow{0}\]
\[\Rightarrow \boxed{ \overrightarrow{Fp_h} = -( \overrightarrow{Fc_h} + \overrightarrow{Ff_h})}\]
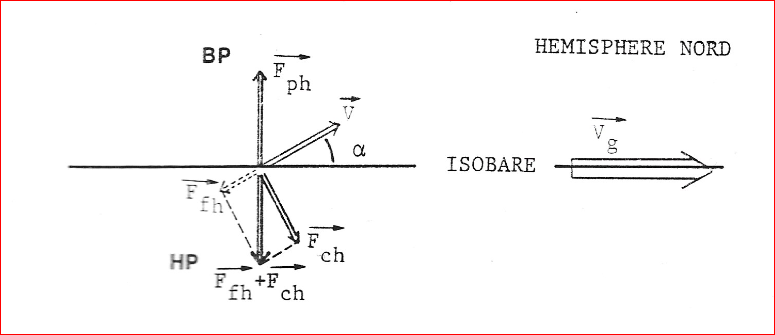
Etudions graphiquement la composition de ces trois forces.
\(\overrightarrow{Ff_h}\) s'oppose au déplacement et est nécessairement vers la gauche (sur notre schéma).
\( \overrightarrow{Fp_h} = -( \overrightarrow{Fc_h} + \overrightarrow{Ff_h})\) \(\Rightarrow\) la force de Coriolis est penchées vers l'avant.
Comme \(\overrightarrow{V}\) est perpendiculaire à \(\overrightarrow{Fc}\), alors nous avons nécessairement l'apparition de l'angle \(\alpha\)
Le vent n'est plus tangent aux isobares, mail il fait un angle \(\alpha\) avec les isobares, et le vent réel est tourné vers la zone de Basse Pression.
\(\alpha\) est fonction de l'importance du frottement. Il a été estimé statistiquement à
- sur mer: \(\alpha \approx10°\)
- sur terrre: \(\alpha \approx 30°\)
L'intensité du vent est aussi affectée. Plus de frottement \(\Leftrightarrow\) Moins de vitesse. Statistiquement:
- sur mer: \(V_{réel} \approx \frac{2}{3}V_g\)
- sur terre: \(V_{réel} \approx \frac{1}{2}V_g\)
Introduction du terme d'accélération \(\overrightarrow{\Gamma_{a_h}}\)
Dans le modèle géostrophique, le mouvement de l'air est considéré comme étant rectiligne et uniforme, c'est à dire \[\overrightarrow{\Gamma_{a_h}}= \overrightarrow{0}\]
Cette condition n'est pas entièrement vérifiée dans la nature.
On constate qu'en général, les accélérations tangentielles sont rares.
Les accélérations perpendiculaires au vecteur vitesse peuvent par contre devenir importantes, notamment lorsque le rayon de courbure des isobares sont faibles.
Nous nous limiterons ici à l'étude d'un cas particulier qui va tenir compte d'un mouvement circulaire à petit rayon de courbure.
\[ \overrightarrow{Fp_h} + \overrightarrow{Fc_h} =m \overrightarrow{\Gamma_{a_h}} \]
\[ \overrightarrow{Fp_h} =m \overrightarrow{\Gamma_{a_h}} -\overrightarrow{Fc_h} = -(\overrightarrow{F_{ch}}+\overrightarrow{F_{centrifuge}})\]
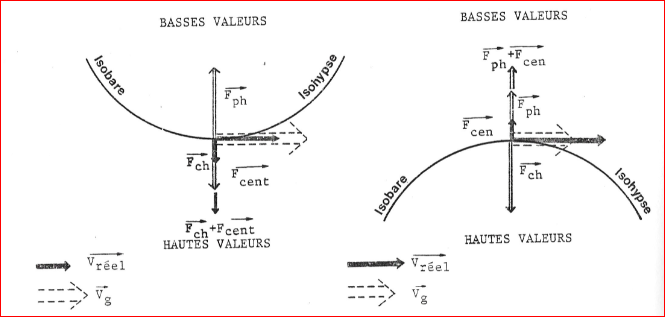
Comme montré dans la figure ci dessous:
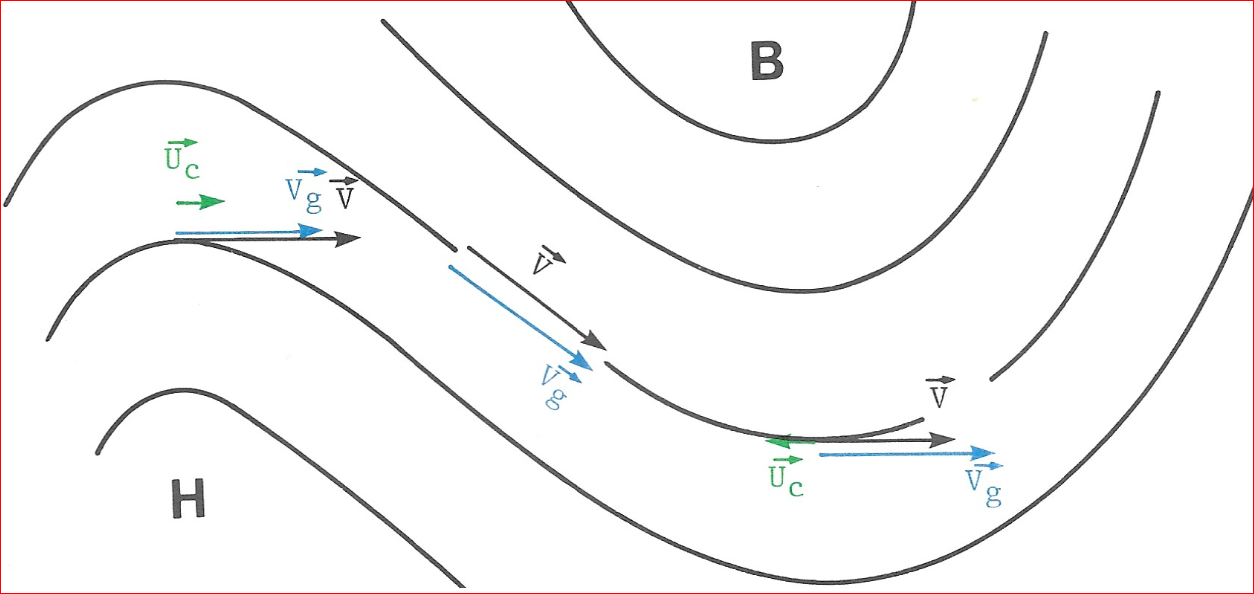
- Dans la courbure cyclonique (à gauche), la force de Coriolis est donc plus faible. Le vent réel est moins fort que le vent géostrophique.
- Dans une courbure anticyclonique (à droite), la force de Coriolis est plus forte et, le vent réel est plus fort que le vent géostrophique..
Un mouvement circulaire est engendré par une accélération centripète.
Cette accélération centripète engendre une force d'inertie qui est centrifuge et qui a pour valeur \(\frac{m V^2}{\Re}\) avec:
m = masse
- V = vitesse
- \(\Re\) = rayon de courbure de la trajectoire
La prise en compte de la force d'inertie centrifuge permet de corriger le vent géostrophique en fonction de la courbure des lignes isobares figurant sur les cartes météo.
On montre que:
\(V_{réel}=Vg \pm \frac{V_g^2}{f \times \Re}\)
avec f = facteur de Coriolis
\(f= 2. \Omega . sin\varphi\)
La correction de courbure
- se retranche à Vg pour pour trouver le vent réel dans une courbure cyclonique (si le centre du cercle est vers la dépression)
- s'ajoute à Vg pour trouver le vent réel dans une courbure anticyclonique
Ordre de grandeur de la correction: 5m/s (10 Kts) pour
- Vg = 10m/s (20Kts)
- à 45° de latitude
- rayon de courbure de 200km
- Vg = vent géostrophique
- V = vent réel