Nous allons ici faire un résumé des formules de trigonométrie. Chaque formule sera écrite, et démontrée.
Formules de bases
Soit un cercle de rayon r = 1 (OA=1) et B un point situé sur ce cercle (OB=1).
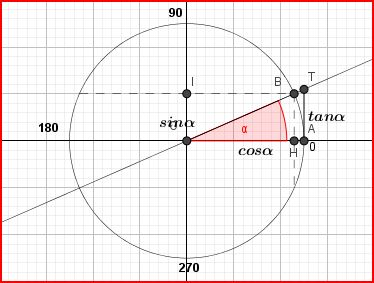
Alors on définit:
\(cos\alpha = \frac{OH}{OB} = OH\) ; \(sin\alpha= \frac{OI}{OB} = OI\) ; \(tan\alpha = \frac{AT}{OA}\)
Moyen mnémotechnique: SOHCAHTOA
- Sin = cote Opposé sur Hypothènue
- Cos = côté Adjascent sur Hypothénuse
- Tan = côté Opposé sur côté Adjascent
Dans le triangle rectangle OHB:
- Appliquons le Théorème de Thalès:
\(tan\alpha = \frac{AT}{OA}=\frac{HB}{OH}=\frac{OI}{OH} \)
\(\Rightarrow \boxed{tan\alpha=\frac{sin\alpha}{cos\alpha}}\)
on définit \(cotan(\alpha) = \frac{1}{tan(\alpha)}= \frac{cos(\alpha)}{sin(\alpha)}\)
- Appliquons le Théorème de Pythagore:
\(OH^2+HB^2 = OB^2\)
\(OH^2+OI^2=r^2=1\)
avec \(OH = cos\alpha\) ; \(OI=sin\alpha\)
Donc: \(\begin{gather}\boxed{cos^2(\alpha)+sin^2(\alpha)=1}\end{gather} \)
Dessinons maintenant le cercle unité avec plusieurs angles remarquables (\(\pi = 180°\)):
\( \boxed{cos(-\alpha)=cos(\alpha)} \space et \space \boxed{sin (-\alpha)=-sin(\alpha)} \)
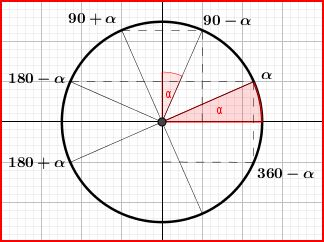
\( \boxed{cos(\pi-\alpha)=-cos(\alpha)} \space et \space \boxed{sin (\pi-\alpha)=sin(\alpha)} \)
\( \boxed{cos(\pi+\alpha)=-cos(\alpha)} \space et \space \boxed{sin (\pi+\alpha)=-sin(\alpha)} \)
\(\boxed{cos(\frac{\pi}{2}+\alpha)=-sin(\alpha)} \space et \space \boxed{sin(\frac{\pi}{2}+ \alpha)=cos(\alpha)}\)
\(\boxed{cos(\frac{\pi}{2}-\alpha)=sin(\alpha)} \space et \space \boxed{sin(\frac{\pi}{2} - \alpha)= cos(\alpha)}\)
En utilisant le théorème de Pythagore, nous avons: \(cos^2(\alpha)+sin^2(\alpha)=1\)
En divisant par \(cos^2\alpha\), il vient: \(\begin{gather}1+\frac{sin^2(\alpha)}{cos^2(\alpha)}=\frac{1}{cos^2\alpha}\end{gather} \Rightarrow \boxed{1 + tan^2(\alpha) = \frac{1}{cos^2(\alpha)}}\)
En divisant par \(sin^2\alpha\) il vient : \(\frac{cos^2(\alpha)}{sin^2(\alpha)}+1=\frac{1}{sin^2(\alpha)} \Rightarrow \boxed{ 1+cotan^2(\alpha) = \frac{1}{sin^2(\alpha)}}\)
Formules d'addition Démonstration
\( \begin{gather} sin(a+b) = sin(a)cos(b)+sin(b)cos(a) \\ cos(a+b) = cos(a)cos(b)-sin(a)sin(b) \\ sin(a-b) = sin(a)cos(b)-sin(b)cos(a) \\ cos(a-b) = cos(a)cos(b)+sin(a)sin(b) \end{gather}\)
Conséquences des formules d'addition
Si a = b, alors:
\(\begin{gather} sin(a+b) = sin(2a) = 2sin(a)cos(a)\end{gather}\)
\(cos(a+b) = cos(2a) = cos^2a-sin^2a \)
Or \(sin^2(\alpha)+cos^2(\alpha)=1\) donc:
\( \begin{gather} cos(2a) =cos^2a-sin^2a = cos^2a-(1-cos^2a) = 2cos^2a-1 \end{gather}\)
\(\Rightarrow \boxed {cos^2a=\frac{1+cos(2a)}{2}} \)
Mais aussi:
\( cos(2a) =cos^2a-sin^2a = 1-sin^2a - sin^2a = 1- 2sin^2a\)
\(\Rightarrow \boxed{sin^2a=\frac{1-cos(2a)}{2}}\)
cos(x), sin(x) et tan(x) en fonction de t = tan(x/2) Démonstration
\(\begin{gather} sinx=\frac{2t}{1+t^2}\\cosx=\frac{1-t}{1+t^2}\\tanx = \frac{2t}{1-t^2} \end{gather}\)
Transformation des sommes en produits Démonstration
\(sinp+sinq=2sin(\frac{p+q}{2})cos(\frac{p-q}{2})\)
\(sinp-sinq=2sin(\frac{p-q}{2})cos(\frac{p+q}{2})\)
\(cosp-cosq=-2 sin(\frac{p+q}{2}) sin(\frac{p-q}{2})\)
\(cosp+cosq= 2 cos(\frac{p+q}{2}) cos(\frac{p-q}{2})\)
Transformation Usuelle Démonstration
Détermination de \(x\) dans l'équation: \(C = Acosx+Bsinx\)
\(\Rightarrow \boxed{ \begin{gather*} C = \rho \times cos(x-\phi) \\ \text{avec: } cos\phi = \frac{A}{\rho} \\ \text{et: } \rho = \sqrt{A^2+B^2} \end{gather*}}\)
Les démonstrations des formules d'addition
Soit les 2 nombres complexes
- z1= cos(a) + isin(a) = eia
- z2= cos(b) + isin(b) = eib
alors z1z2 = eia x eib = ei(a+b) = cos(a+b) + isin(a+b)
- La partie réelle de z1z2, R(z1z2) = cos(a+b)
- La partie imaginaire de z1z2, I(z1z2) = sin(a+b)
Calculons z1z2:
z1z2 = (cosa + isina) x (cosb + isinb)
z1z2 = cosa cosb + i cosa sinb + i sina cosb - sina sinb
z1z2 = (cosa cosb - sina sinb) + i (sina cosb + cosa sinb)
\[ I(z_1z_2) = sin(a+b) = sina cosb + cosa sinb \text{ (3)} \]
\[ R(z_1z_2) = cos(a+b) = cosa cosb - sina sinb \text{ (4)} \]
Remplaçons b par (-b) dans (3) et (4) et appliquons les formules de bases de trigonométrie:
- cos(-b) = cos(b)
- sin(-b) = -sin(b)
Alors :
sin(a-b) = sina cos(-b) + cosa sin(-b) (3)
\[ sin(a-b) = sina cosb - cosa sinb \text{ (5)} \]
Et:
cos(a-b) = cosa cos(-b) - sina sin(-b) (4)
\[ cos(a-b) = cosa cosb + sina sinb \text{ (6)} \]
Démonstration de cos(x), sin(x) et tan(x) en fonction de t = tan(x/2)
\(\text{(7): }sin(2a) = 2sinacosa\)
\(\Rightarrow sinx = 2sin\frac{x}{2}cos\frac{x}{2}\)
\( \Rightarrow sinx=2sin\frac{x}{2}cos\frac{x}{2} \times \frac{cos\frac{x}{2}}{cos\frac{x}{2}}= 2tan\frac{x}{2}cos^2\frac{x}{2}\)
\(\text{(2): } tan^2x+1=\frac{1}{cos^2x} \Rightarrow cos^2x=\frac{1}{1+tan^2x}\)
\(\Rightarrow sinx = 2 tan\frac{x}{2} \times \frac{1}{1+tan^2\frac{x}{2}}= \frac{2t}{1+t^2}\)
\(\text{(8): } cos2a=2cos^2a-1 \Rightarrow cosx = 2cos^2\frac{x}{2} - 1\)
\(\text{(2): } tan^2x+1=\frac{1}{cos^2x} \Rightarrow cos^2x=\frac{1}{1+tan^2x}\)
\( \Rightarrow cosx =2 \times \frac{1}{1+tan^2\frac{x}{2}} - 1 = \frac{2-1-tan^2\frac{x}{2}}{1+tan^2\frac{x}{2}}=\frac{1-t^2}{1+t^2}\)
\(tanx=\frac{sinx}{cosx}=\frac{\frac{2t}{1+t^2}}{\frac{1-t^2}{1+t^2}}=\frac{2t}{1-t^2}\)
Démonstration des transformations de sommes en produits
en additionnant (3) et (5), il vient:
sin(a+b) + sin(a-b) = 2 sina cosb
posons:
- p=a+b
- q=a-b
alors en additionnant ces 2 termes, puis en les soustrayant, nous avons:
\(a=\frac{p+q}{2} \text { et } b = \frac{p-q}{2}\) et ensuite:
\(sin(a+b) + sin(a-b) = 2 sina cosb\)
\(\Rightarrow sin(\frac{p+q}{2}+\frac{p-q}{2}) + sin(\frac{p+q}{2}-\frac{p-q}{2}) = 2 sin\frac{p+q}{2} cos \frac{p-q}{2}\)
\(\Rightarrow sinp + sinq = 2 sin\frac{p+q}{2} cos \frac{p-q}{2}\)
On procède de même pour les autres additions ou soustraction.
(3) - (5) \(\Rightarrow\) sin(a+b) - sin(a-b) = 2 sinb cosa
\(\Rightarrow sin(\frac{p+q}{2}+\frac{p-q}{2}) - sin(\frac{p+q}{2}-\frac{p-q}{2}) = 2 sin\frac{p-q}{2} cos\frac{p+q}{2}\)
\(\Rightarrow sinp - sinq = 2 sin\frac{p-q}{2} cos\frac{p+q}{2}\)
(4) - (6) \(\Rightarrow\) cos(a+b) - cos(a-b) = -2 sina sinb
\(\Rightarrow cosp-cosq=-2 sin\frac{p+q}{2} sin\frac{p-q}{2}\)
(4) + (6) \(\Rightarrow\) cos(a+b) + cos(a-b) = 2 cosa cosb
\(\Rightarrow cosp+cosq= 2 cos\frac{p+q}{2} cos\frac{p-q}{2}\)
Démonstration de la formule usuelle
Il s'agit de résoudre l'équation suivante: C = A cosx + B sinx
\( C = Acosx+Bsinx = \sqrt{A^2+B^2}(\frac{A}{\sqrt{A^2+B^2}}cosx + \frac{B}{\sqrt{A^2+B^2}}sinx)\)
Posons \(\rho = \sqrt{A^2+B^2}\), alors
\(C = \rho (\frac{A}{\rho}cosx + \frac{B}{\rho}sinx)\)
Posons maintenant: \(\frac{A}{\rho} = cos\phi\), alors \(\frac{B}{\rho} = sin\phi\)
En effet: \(cos^2\phi + sin^2\phi = \frac{A^2}{\rho^2} + \frac{B^2}{\rho^2} = \frac{A^2+B^2}{\sqrt{A^2+B^2}^2} = 1\)
Alors:
\(C = \rho (cos\phi cosx + sin\phi sinx)\)
Or (6) \(\Rightarrow\) cos(a-b) = cosa cosb + sina sinb
\(\Rightarrow \boxed{ \begin{gather*} C = \rho \times cos(x-\phi) \\ \text{avec: } cos\phi = \frac{A}{\rho} \\ \text{Et: } \rho = \sqrt{A^2+B^2} \end{gather*}}\)