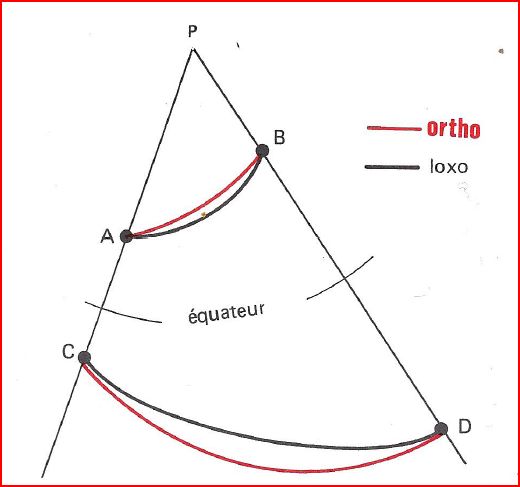
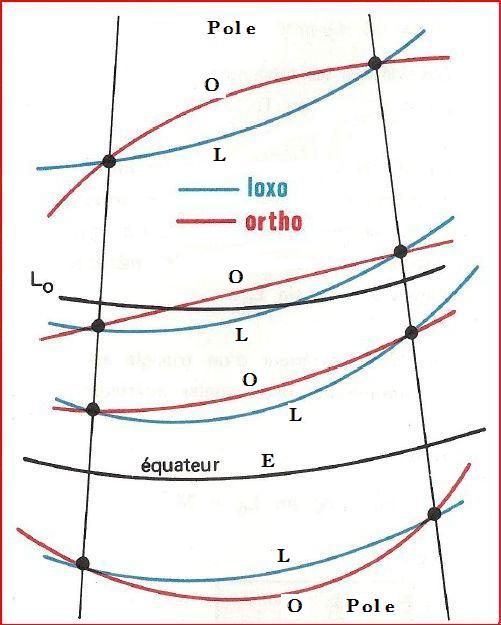
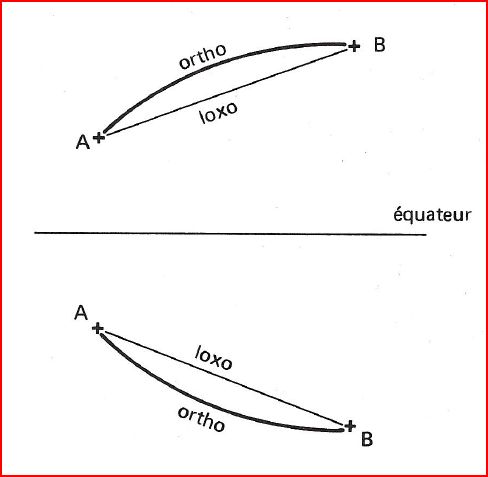
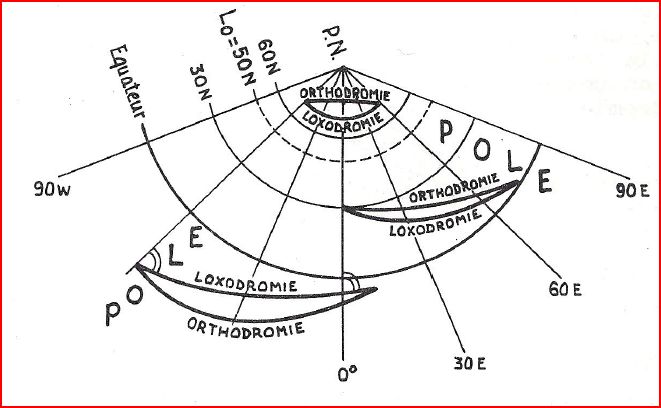
Maintenant que nous avons vu les 3 canevas principaux que vous pourriez rencontrer, il s'agit de voir l'allure des routes loxodromique et orthodromique sur ces cartes, ainsi que le sens de leurs courbures, leurs positions relatives.
Il conviendra ensuite de vous donner les moyens de retenir les angles entre ces routes et la droite carte.
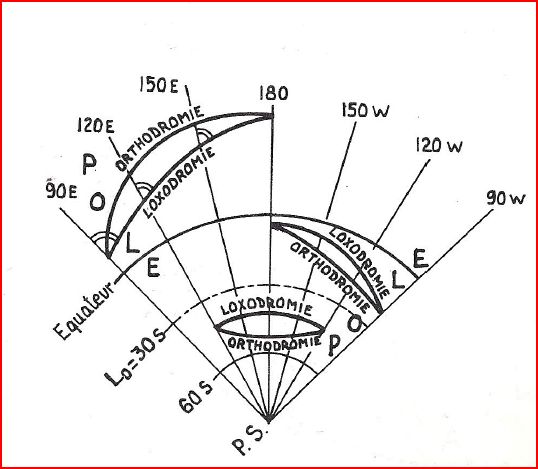
La régle POLE
Comme montré sur la figure, on aura toujours les courbes représentées dans cet ordre:
- Pole Nord
- Ortho
- Loxo
- Equateur
- Loxo
- Ortho
- Pole Sud
La courbure des loxo et ortho
La loxodromie tourne toujours sa concavité vers un Pôle
L'orthodromie tourne toujours sa concavité vers le lieu d'Echelle minimum:
L'Echelle minimum se situe à la latitude à laquelle le plan de projection est tangent à la sphère réduite.
- vers l'équateur sur un canevas Mercator (L=0)
- vers L0 sur un canevas Lambert (sauf au voisinage de L0 car l'ortho est représentée par une droite carte)
- vers le Pôle du plan tangent (N ou S) sur un canevas stéréopolaire (L=90)
Quelques exemples:
Sur un canevas Mercator L0 = 0
Sur un canevas Lambert (L0 = 50N)
Sur un canevas Lambert (L0 = 30S)
Les angles entre les routes
Nous avons défini dans les chapitres précédents plusieurs angles:
- V = angle de route de la loxo
- γ = l'angle entre ortho et loxo (correction de Givry)
- u = angle entre ortho et droite carte (pseudo correction de Givry)
- δ = angle entre droite carte et loxo
Afin de mémoriser comment calculer ces angles, on peut partir de leurs calculs effectués pour un canevas Lambert tangent en L0, et en suite pousser L0 à ses extrèmes, c'est à dire:
- L0 = 0 pour un canevas Mercator
- L0 = L0 pour un canevas Lambert
- L0 = 90 pour un canevas stéréopolaire
Angle de route Loxo RV dépend de α
Quelque soit le canevas, la loxo fait un angle constant avec les méridiens.
Cet angle est tel que \[\boxed{tanα = \frac{dg}{ΔL_c} \space \# \space \frac{dg \times cosL_m}{ΔL}}\]
ΔR = Convergence des méridiens
\[\boxed{ΔR = Rv_B - Rv_A \space \# \space dg \times sinL_m}\]
Angle γ entre otho et loxo = correction de Givry
Quelque soit le canevas, cet angle est toujours le même: \[\boxed {γ = \frac{dg}{2} \times sinL_m = \frac{ΔR}{2}}\]
Angle u entre ortho et droite carte = pseudo correction de Givry
Pour un canevas Lambert tangent en L0: \[\boxed {u =\frac{dg}{2} \times (SinL_m - sin L_0)}\]
- si L0 = 0, sinL0 = 0, et \(u = \frac{dg}{2} \times sinL_m = γ\), ce qui est normal puisque la droite carte est la loxo
- si L0 = 90, sinL0 = 1, et \(u =\frac{dg}{2} \times (SinL_m - 1)\)
Angle δ entre loxo et droite carte
Pour un canevas Lambert tangent en L0: \[\boxed {δ = \frac{dg}{2} \times sinL_0}\]
- si L0 = 0, sinL0 = 0, et δ = 0, ce qui est normal puisque la droite carte est une loxo
- si L0 = 90, sinL0 = 1, et \(δ = \frac{dg}{2}\)
Et on a toujours :
\[\boxed{γ =u + δ}\]
Et pour rappel, la flèche max entre ortho et loxo: \[\boxed {f^{MN}=\frac{γ° \times D}{230}}\]