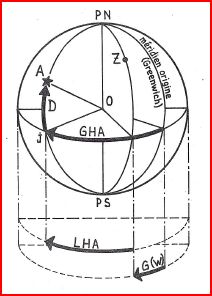
Il est possible de se positionner lorsque l'astre que l'on relève passe sur le méridien de l'observateur. En général, on utilise le soleil pour connaître sa position, mais il est possible d'utiliser n'importe quel astre. Dans l'ordre, expliquons:
- ce qui se passe
- la démonstration pour la longitude
- la démonstration pour la latitude
- Comment faire dans la pratique
Voyons ce qui se passe avec le Soleil:
Le Soleil est sur le mérdien de l'observateur:
- il est 12h00 Tcg
- LHASoleil = 0
Nous sommes capables de déterminer notre longitude.
- P=0
- Le Soleil est au Nord de l'observateur, ou
- Le Soleil est au Sud de l'observateur
Nous sommes capables de déterminer notre latitude si nous connaissons Hv.
La longitude méridienne
La longitude méridienne est la différence entre l'heure de passage de l'astre au méridien de l'observateur et l'heure de passage de l'astre au méridien de Greenwich.
Notre marin doit connaître l'heure exacte.
Lorsque le Soleil passe au méridien de l'observateur, alors:
- LHASoleil = 0 \[\Rightarrow \boxed{ G(W) = GHA_{Soleil} \text{à l'instant t}}\]
La latitude méridienne
C'est la mesure la plus simple. Elle est utilisée depuis l'antiquité car il n'est pas besoin de connaître l'heure exactement.
La latitude méridienne s'obtient en mesurant la hauteur du Soleil au-dessus de l'horizon, lorsqu'il est au plus haut. A ce moment précis LHASoleil = 0,
cos(90-H) = cos(90-D) cos(90-L) + sin(90-D) sin(90-L) cosP avec cos P = 1
\(\Rightarrow\)cos(90-H) = cos[(90-D)-(90-L)]
\(\Rightarrow\) cos(90-H) = cos(L-D) = cosα
avec 90-H >0, \(\Rightarrow\) α > 0, et cosα = cos(-α)
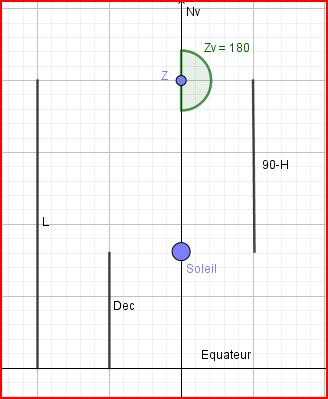
- Si L>D, alors Z = 180, le Soleil est au Sud de la position ou l'observateur a le Nord dans le dos
alors L - D > 0
cos(90-H) = cos(L-D) \(\Rightarrow\) 90-H = L - D
\(\Rightarrow\) L= D+(90-H)
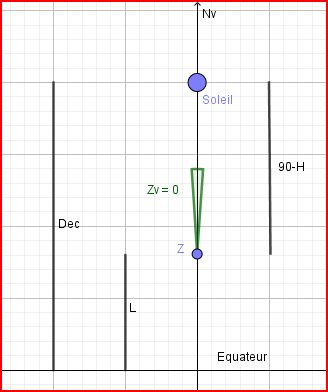
- Si L<D,alors Z = 0, le Soleil est au Nord de la position ou l'observateur a le Sud dans le dos
alors D - L > 0
cos(90-H) = cos(D-L) \(\Rightarrow\) 90-H = D - L
\(\Rightarrow\) L= D-(90-H)
\[\boxed{ L = D+/- (90-Hv)} \\ \text{+ si observation avec le Nord dans le dos} \\ \text{- si observation avec le Sud dans le dos} \]
Et dans la pratique
Dans la pratique, la navigation est suivie, le marin connait alors sa position approximative, car il connait:
- La position de son dernier point
- La route et la vitesse suivie approximativement de puis le dernier point
Comme il connait approximativement sa position, il sait a peu près à quelle heure il va pouvoir faire sa méridienne, soit l'heure H
A H-15 minutes, il mesure la hauteur du soleil (montant), bloque son sextant, et note l'heure H1
Autour de l'heure H, le Soleil reste environ 1 minute à la même hauteur. Si on peut mesurer Hv, il est difficile de mesurer l'heure.
Avant H+15 minutes, il regarde le soleil au sextant et il attend que le soleil redescende à la même hauteur qu'à H-15 min. Au moment ou le soleil est à la même hauteur qu'a H-15, il note l'heure H2.
Le soleil est passé au méridien de l'observateur à l'heure moyenne \(H'=\frac{H_2 + H_1}{2} = H1 + \frac{\Delta H}{2}\)
Il suffit alors de transformer cette heure H' en G(W) à l'aide des éphémérides.
On peut faire plusieur mesures dans cet esprit. Dans ce cas, l'heure sera \(H'=\frac{h_1+h_2+h_3+h_4}{4}\).
Certains preconisent de tracer un graphique représentant la Hauteur de L'astre en fonction dey temps, ce qui permettra de trouver graphiquement l'heure, et la hauteur max de l'astre et d'en déduire de la même façon sa Latitude et sa Longitude.