Afin de simplifier les calculs, Dieumegard et Bataille ont mis les équations de trigonométrie sphérique sous une autre forme. Cette nouvelle forme a permis l'édition de tables de calculs ne nécessitant pas de calculatrice pour trouver sa position. Il suffira de rentrer dans des tableaux avec les données connues: L, D, P, pour déterminer Hc (la hauteur calculée), et Zc (l'azimut calculé).
- Les tables de Dieumegard permettent de déterminer Hc
- Les tables de Bataille permettent de déterminer Zc
Les tables de Dieumegard
Ces tables permettent de trouver la hauteur calculée Hc en utilisant une formule particulière, différente de la formule habituelle. Elles se présentent sous la forme de 29 tableaux de chiffres, divisés en 4 groupes :
- La table 1 (12 pages) donne un premier chiffre (a1) à partir de l'angle horaire local LHA (heure de mesure + éphémérides);
- La table 2 (5 pages) donne un second nombre (a2) et un troisième nombre (a3) à partir de la latitude estimée de l'observateur L et de la déclinaison de l'astre D ;
- La table 3 (6 pages) donne un quatrième chiffre (a4) à partir de la somme S1 = a2 + a3 + a1;
- La table A (6 pages) donne un cinquième chiffre (a5) à partir de notre latitude L et de la déclinaison D, puis, enfin, la Hauteur calculée à partir de la somme S2 = a4 + a5
Les tables de Bataille
Ces tables permettent de calculer que l'Azimut Zc. C'est pourquoi elles complètent parfaitement les tables de Dieumegard et qu'elles y sont la plupart du temps associées. D'autant plus que le mode d'emploi de ces deux tables est très semblable. Cependant, comme vous allez le voir, elles sont totalement indépendantes.
Les tables de Bataille se présentent sous la forme de 10 tableaux de chiffres divisés en 2 groupes :
- La table 1 (4 pages) permet de transformer l'angle au pôle P et notre latitude estimée L en un premier chiffre (m).
- La table 2 (6 pages) permet de transformer la déclinaison D et notre latitude estimée L en un second chiffre (n).
On additionne m + n = S3 .
Enfin, muni de S3 et de P, on revient dans la table 2 pour trouver la valeur de l'azimut Zc.
Point de départ des tables de Dieumegard et Bataille
On utilise toujours les 3 mêmes paramètres de départ : Latitude estimée (L), Angle horaire local (LHA) et Déclinaison (D).
Encore un petit effort pour comprendre comment sont construites ces tables........... La démonstration nécessite un peu de concentration, mais cela permettra de comprendre les tables de Dieumegard et Bataille, dont l'utilisation est très simple
Pour la suite, vous pouvez vous référer au Précis de trigonométrie et à la Trigonométrie sphérique.
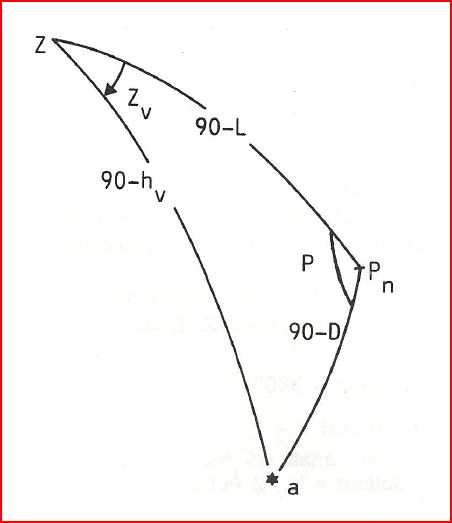
Rappelons nous simplement 3 formules de trigonométrie sphérique permettant d'exprimer Hc et Zv:
La formule fondamentale:
\[\boxed{ cos(90-H_c) = cos(90-L) \times cos(90-D) + sin(90-L) \times sin(90-D) \times cosP}\]
La formule des 4 éléments consécutifs:
\(C_e \space S_i \space cotés = C_e \space S_i \space angles + Cos_i \space Cos_i\)
\[ \boxed{cotan(90-D) \times sin(90-L)= cotanZ_v \times ZsinP + cos(90-L) \times cosP}\]
et l'analogie des sinus qui nous donne:
\[\boxed{\frac{sinP}{sin(90-Hv)}=\frac{sinZ}{sin(90-D)}}\]