Le principe de la navigation astronomique consiste à comparer la hauteur de l'astre que l'on devrait observer avec le sextant si on était là où on pense être (Hc = Hauteur calculéé), avec ce qu'on observe en réalité (Hv = hauteur vraie), et corriger son estime en conséquence. On passe donc d'une droite de position estimée reportée sur la carte, à une droite position réelle mesurée au sextant, qu'on reportera sur cette même carte.
Ce principe repose sur:
- la connaissance du temps à la seconde prés (connaître l'heure au méridien de Greenwich avec une grande précision ne pose plus de problème aujourd'hui avec les montres à quartz)
- la position de l'astre observé (grâce à l'heure du relevé et aux éphémérides)
- la position estimée de l'observateur (en connaissant la route, le temps, et la vitesse depuis le dernier point)
- la hauteur de l'astre observé (mesure au sextant)
Comment faire
Entretenons notre position « estimée », c'est-à-dire calculons notre position à partir du dernier point solidement déterminé à proximité des côtes (en estimant la vitesse et la route suivie pendant un certain temps).
Cette position estimée sera légèrement différente de notre vraie position en raison des éléments de dérive qui nous écartent de notre route. Ils sont dus aux vents et aux courants, à une tenue de cap plus ou moins précise, etc etc ... Le fin navigateur essayera de deviner cette dérive, par calculs, observation, connaissance de son navire. Mais plus le temps passe, moins la position est précise. Il faudra « recaler notre estime ».
Nous allons dans un premier temps considérer que la position estimée n’est pas si mauvaise que cela, et n’est pas trop éloignée de notre position vraie. Nous pouvons marquer cette position estimée sur notre carte.
C’est à ce moment que nous sortons notre sextant pour mesurer l’angle entre nous (observateur), l’horizon, et un astre pour obtenir sa « hauteur vraie ». (Hvraie = Hmesurée + corrections)
Notons que notre opération nécessite une très grande maîtrise de la mesure du temps. C’est d’ailleurs la raison pour laquelle les navigateurs ont attendu des siècles avant de pouvoir faire ce genre de calcul.
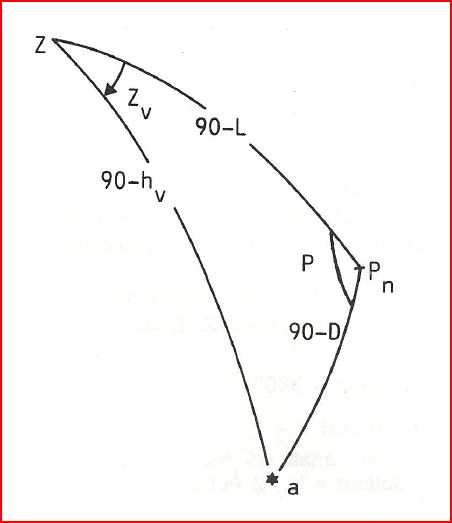
A partir de la position estimée (longitude G et latitude L), et de l'heure, qui nous donneront D (la déclinaison de l'astre) et GHA (le méridien de l'astre) lus dans les éphémérides, on pourra calculer P (angle entre notre méridien et celui de l'astre) et Hc (hauteur calculée).
Hc et Zc sont calculés grâce à la résolution d’un triangle sphérique dont les sommets sont l’astre, le pôle élevé (Nord ou Sud) et le zénith de l’observateur et dont les côtés sont la distance zénithale, la co-latitude et la distance polaire.
La formule fondamentale (Trigonométrie sphérique) :
\( cos(90-H) = cos(90-L)cos(90-D) + sin(90-L)sin(90-D)cosP\)
\[\Rightarrow \boxed{sinH=sinLsinD+cosLcosDcosP}\]
La formule des 4 éléments consécutifs (Trigonométrie sphérique) :
\[ \boxed {CeSi côté = CeSi angle + cosi cosi }\]
- Nous avons calculé l'azimut de l'astre (angle entre le Pole, l'observateur et l'astre)
- Nous avons calculé Hc, qui correspond au cercle sur lequel nous pensons être.
- Nous avons mesuré Hv, qui correspond au cercle sur lequel nous sommes réellement.
- En calculant Hv-Hc, nous connaissons la distance en MN entre ces 2 cercles (aussi appelé Intercept)
- Nous pouvons tracer une droite de hauteur