Une carte, pour être exploitable en navigation, doit vérifier un certain nombre de propriétés sur toute l'étendue de sa surface, ou sur certaines parties, soit rigoureusement, soit approximativement. Elle doit être:
- conforme
- équidistante
- équivalente
Elle pourra avoir d'autres propriétés comme par exemple être:
- loxodromique
- orthodromique
Nous allons aussi voir ce que sont
- L'échelle d'une carte
- L'unité d'une carte
- Les conditions à vérifier pour qu'une carte soit conforme
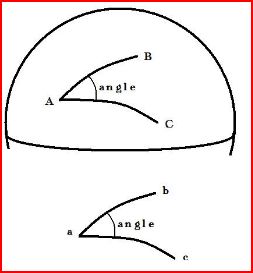
Une carte conforme
A un angle α sur la carte doit correspondre le même angle α sur la Terre
Ce canevas conserve les angles
Cette qualité est essentielle et indispensable pour une carte de navigation. De toute évidence, sans cette qualité, une carte ne serait pas utilisable pour déterminer et suivre une route simplement.
Un canevas conforme a pour propriété de présenter une échelle constante dans toutes les directions autour d'un point. Ce qui veut dire qu'un carré ou un cercle de petites dimensions seront représentés sur la carte par un carré ou un cercle, et non pas par un parallélogramme ou une ellipse. Une carte tracée sur un canevas conforme conservera l'allure et la forme des objets.
Cette propriété permet une identification des objets plus facile en même temps qu'elle permet des mesures de distance sur des routes orientées différemment.
De façon générale, toutes les cartes utilisées en navigation sont rigoureusement conformes sur toute l'étendue de leur surface.
On remarquera que sur un canevas conforme, les méridiens et les parallèles se coupent toujours perpendiculairement, et ce, même si ils ne sont pas représentés par des lignes droites.
Une carte équidistante
A une même longueur sur la carte correspond une même longueur sur la Terre.
Il n'existe pas de système de projection qui conserve constant le rapport des longueurs (sinon une sphère serait développable!!).Pourtant cette propriété serait bien pratique pour la mesure des distances.
Les cartes de navigation ne sont donc pas équidistantes. Par contre, elles sont en général à peu près équidistantes si on considère des points peu éloignés.
\(\mathrm{ \frac{ab}{AB} = \frac{ac}{AC}} = constante\)
Une carte équivalente
A une même surface sur la carte correspond une même surface sur la Terre.
On démontre aisément que si une carte est conforme et qu'elle n'est pas équidistante, elle ne peut pas être équivalente.
\(\mathrm{ \frac{s_1}{S_1} = \frac{s_2}{S_2}} = constante\)
Des canevas équivalents existent (Bonne), mais ils ne présentent aucun intérêt pour la navigation et ne sont, en conséquence, pas utilisés.
Une carte orthodromique
Une carte est dite orthodromique si toute orthodromie sur la Terre est représentée rigoureusement par une droite sur la carte.
L'intérêt d'un canevas orthodromique pour certains types de navigation est évident, l'orthodromie étant la route la plus courte entre 2 points de la Terre. Il existe plusieurs canevas orthodromiques, dont
- le canevas gnomonique
- le canevas Lambert conique (au voisinage du parallèle de tangence, Mercator Oblique au voisinage du grand cercle de contact).
Une carte loxodromique
Une carte est dite loxodromique si toute loxodromie sur la Terre est représentée rigoureusement par une droite sur la carte.
Une loxodromie est la route à cap constant la plus courte entre 2 points sur la Terre.
C'est un des premiers canevas qui ait été réalisé. Le canevas Mercator Direct par exemple est un canevas loxodromique.
Echelle d'une carte
L'échelle d'une carte est le rapport des longueurs, exprimées dans la même unité, entre une distance sur la carte et la distance correspondante sur Terre. L'Echelle est donc une grandeur sans unité.
\(\mathrm{E=\frac{ab^{mm}}{AB^{mm}}= \frac{1}{\frac{AB}{ab} } }\)
Nous avons vu plus haut qu'il n'existait pas de carte rigoureusement équidistante. Donc il n'existe pas de carte d'échelle rigoureusement constante. Lorsque l'on parle d'échelle d'une carte, il faut toujours préciser le lieu où l'échelle possède cette valeur. Par exemple on lira sur la carte 7033 de la Baie de Quiberon": Echelle 1:50000 en 47°30'N.
L'Echelle est sans unité, c'est à dire que 1 cm sur la carte représente 50 000 cm sur Terre mais aussi, que 1mm sur la carte représente 50 000 mm sur Terre.
Pour trouver l'échelle d'une carte en 1 point de latitude L, il suffit de mesurer sur la carte, sur le méridien, la distance d en mm entre le paralélle L+1° et L-1° par exemple.
La distance sur la terre est égale à 2° sur un grand cercle, donc 2 x 60' = 120 MN = 120 x 1852 x 1000 mm.
Alors l'échelle sera:
\(\mathrm{E_L=\frac{d}{AB}= \frac{1}{\frac{120\times1852\times1000}{d} } }\)
Voici un extrait de la carte 7033 "Baie de Quiberon"
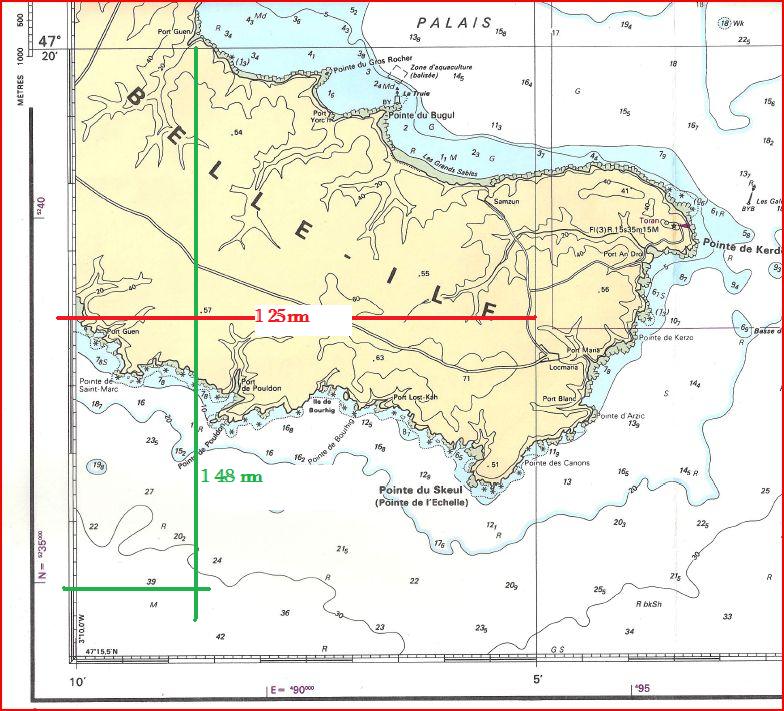
Calculons l'échelle de cette carte (tracé vert):
4 minutes d'arc sur le méridien (grand cercle) = 4 MN représentés par 148 mm
\(\mathrm{E_L=\frac{d}{AB}= \frac{1}{\frac{4\times1852\times1000}{148} } = \frac{1}{50054} }\)
L'échelle donnée par l'éditeur est 1/50 000 ème. L'écart est du à la précision de la mesure.
L'unité d'une carte
L'unité d'une carte est égale au rapport des longueurs entre une distance sur la carte exprimée en mm et la distance correspondante sur la Terre exprimée en MN.
\(\mathrm{U = \frac{ab^{mm}}{AB^{MN}}}\)
Tout comme pour l'échelle, lorsqu'on parle d'unité d'une carte, il convient de préciser le lieu où l'unité a cette valeur.
Un abus de langage pourrait faire dire: cette carte a pour échelle 15mm pour 45MN à la latitude N20°. En fait, c'est bien de l'unité dont il est question ici.
Dans notre cas, on peut écrire
\(\mathrm{U_{47} = \frac{148^{mm}}{4^{MN}} = 37mm/MN}\)
Condition de conformité
On démontre que pour qu'une carte soit conforme il faut et il suffit qu'au voisinage d'un point quelconque, l'échelle soit la même en suivant deux directions perpendiculaires. Pour vérifier la conformité d'une carte, on prendra, en général, comme direction:
- le méridien
- le parallèle
On calculera les échelles dans les 2 directions et on les comparera. Si elles sont égales, alors la carte sera conforme.
Nous avons déjà calculé EL = 1/50 000
Calculons EM
Distance terre = 5 x 1852 x 1000 x cos(47,5) mm
Distance carte = 125 mmm
\(\mathrm{E_M= \frac{1}{\frac{5\times1852\times1000\times cos47,5}{125} } = \frac{1}{50048} }\)
EL = EM = 1:50 000, à l'erreur de mesure près, donc la carte est conforme.

