Le Théorème de l'Arc Capable:
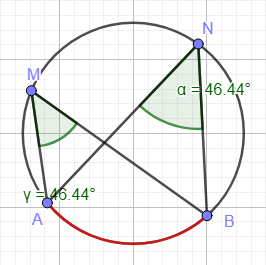
Il répond à la question suivante: étant donnés deux points A et B, quel est l'ensemble des points M du plan tel que l'angle \(\widehat {AMB}\) soit égal à un angle de valeur constante donnée α ?
Le lieu des points M répondant à cette question est un cercle contenant A, B et M. On dit que AB est vu depuis l'arc sous un angle α, ou encore que l'arc de cercle AB est capable d'inscrire un angle de mesure α.
Vous pouvez voir ce qui se passe en faisant bouger les points M ou N (cliquez ici ou sur la figure). On constate que les angles en M et N restent constants et égaux quelquesoient les positions de M ou N.
Ce qui signifie que lorsqu'on voit les amers A et B sous un angle α, alors nous nous situons sur un cercle contenant les points A, B, M.
Si on considère 3 amers A, B, et C, il est possible depuis le bateau de mesurer les angles sous lesquels on voit les arcs AB, puis BC (ou n'importe quelle combinaison entre ces 3 points).
Alors on peut tracer 2 cercles, et nous nous situons à l'intersection de ces 2 cercles.
Mais comment tracer ces 2 cercles?
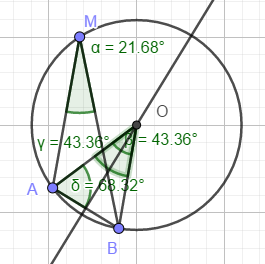
Le Théorème de l'angle au centre
Considérons un cercle contenant les points A, B, M.
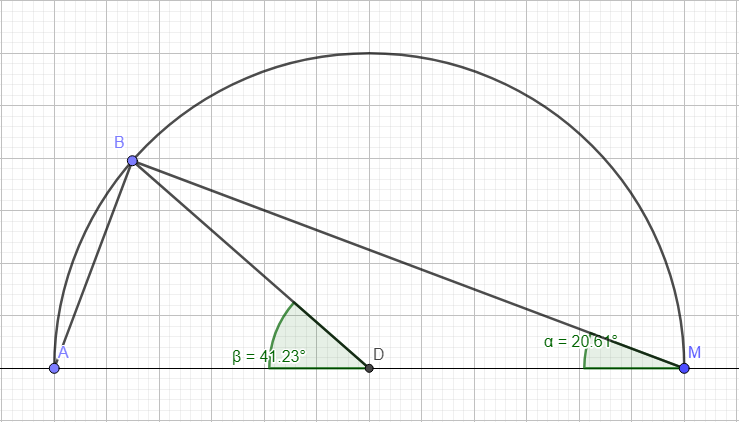
Alors l'angle \(\widehat {AOB}\) = 2 x \(\widehat {AMB}\)
Connaissant, A, B, et l'angle α , il est possible de déterminer O et de tracer le cercle de centre O et de rayon OA, OM, ou OB représentant les lieux M, position du bateau.
En cliquant sur l'image, faites bouger les points A ou B pour faire varier l'angle α
Trouver le centre du cercle
Soient les points A et B sur un cercle et α l'angle sous lequel on voit A, et B.
Alors le centre du cercle, position de M est à l'intersection:
- de la médiatrice de AB
- et de la droite issue de A ou B, faisant un angle de (90 - α) avec le segment AB
Utilisation
Donnons nous 3 amers A, B, C
A l'aide d'un sextant tenu à l'horizontale, ou en faisant la différence entre 2 relèvements fait au compas de relèvement, mesurons les angles sous lesquels ont voit:
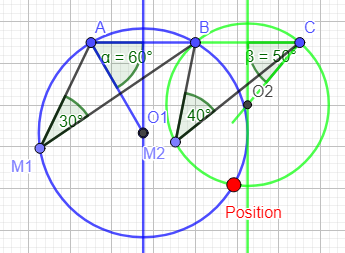
- l'arc AB: α = 30°
- l'arc BC: β = 40°
- les segments AB, et BC
- les médiatrices des segments AB et BC
- une droite issue de A formant un angle de 90 - 30 = 60° pour trouvers O1 le centre du 1er cercle (bleu)
- une droite issue de C formant un angle de 90 - 40 = 50° pour trouver O2 le centre du 2ème cercle (vert)
- le cercle de centre O1 et de rayon O1A ou O1B
- le cercle de centre O2 et de rayon O2B ou O2C
En mesurant l'angle sous lequel on voit les arcs AB et BC, on peut vérifier notre tracé. Nous devrions trouver respectivement 30° et 40° (noir)
La pratique
Pour le moment, pour faire le point avec la méthode des arcs capables, il est nécessire d'avoir un compas pour tracer les cercles. Nous allons voir comment nous en passer:
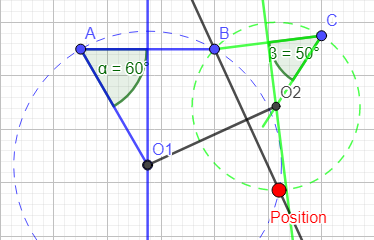
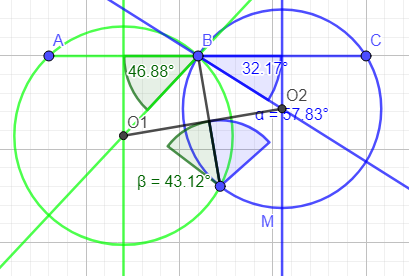
Traçons:
- le segment O1O2
- la perpendiculaire au segement O1O2 passant par B
- M est le symétrique de B par rapport au segment O1O2
