Que mesure t-on en mesurant la hauteur d'un astre?
Une distance
On utilise un sextant pour mesurer une distance entre un bateau et un amer dont la hauteur est connue
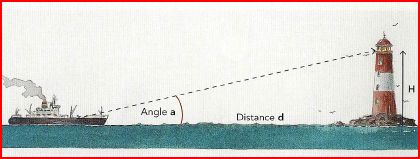
Connaissant la hauteur H, et l'angle a, on détermine la distance d
\(tan(a) = \frac{H}{d} \Rightarrow d= \frac{H}{tan (a)}\) avec d et h en mètres.
Hors:
\(d_m=d_{MN} \times 1852 \\ tan (a_{rd}) = (a_{rd})= \frac{a' \times \pi}{180 \times 60} \\ \Rightarrow d_{MN} = \frac{H_m \times 180 \times 60}{1852 \times a' \times \pi} \\ \Rightarrow \boxed{d_{milles} = \frac{1.86 \times H_{metres}}{a_{minutes}}}\)
Le cercle de position
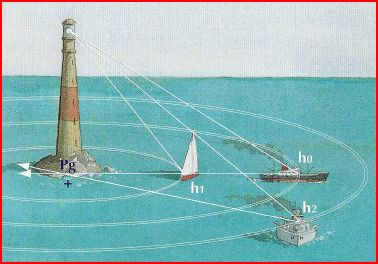
- Depuis le cargo, le phare est vu sous un angle h0
- Depuis le voilier: h1 >h0, le voilier est plus près du pied du phare que le cargo
- Depuis le bâtiment de guerre, h2 < h0, le croiseur est plus éloigné du pied du phare que le cargo
Ces navires sont positionnés sur un cercle dont le rayon dépend directement de la hauteur mesurée au sextant
On comprend alors qu'en mesurant la hauteur d'un astre, on définit la distance entre le pied de l'astre et la position du bateau.
Etant donnée la distance entre le pied de l'astre et le bateau, on pourra assimiler la portion de cercle qui nous interesse à une droite appelée droite de hauteur.
Par convention, l'axe "navire" - "pied de l'astre" sera orienté positivement depuis le navire vers le pied de l'astre